前提条件
3次元空間において、法線ベクトル\vec{n}、平面を通る点Aで表現される平面に対し、ベクトル\vec{v}を投影した平面上のベクトル\vec{v’}を求めることを想定します。
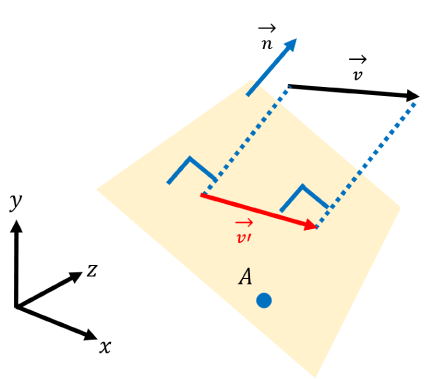
平面に投影したベクトルを求める式
平面に投影したベクトル\vec{v’}は、次式で求められます。
平面に投影したベクトル
\vec{v'} = \vec{v} - \frac{\vec{n} \cdot \vec{v}}{|\vec{n}|^2} \vec{n}ただし、|\vec{n}| \neq 0
特に、|\vec{n}|=1すなわち法線ベクトル\vec{n}が正規化されたとき、次式で表されます。
平面に投影したベクトル(法線ベクトルが正規化された場合)
\vec{v'} = \vec{v} - (\vec{n} \cdot \vec{v}) \vec{n}平面に投影したベクトルのxyz成分
法線ベクトル\vec{n}、点A、ベクトル\vec{v}をそれぞれ、
\vec{n} = \left( \begin{array}{c} n_x \\ n_y \\ n_z \end{array} \right) ,
A = \left( \begin{array}{c} a_x \\ a_y \\ a_z \end{array} \right) ,
\vec{v} = \left( \begin{array}{c} v_x \\ v_y \\ v_z \end{array} \right)とすると、平面に投影したベクトル\vec{v’}のxyz成分は次のように表されます。
平面に投影したベクトルのxyz成分
\vec{v'} = \left( \begin{array}{c}
v_x - s n_x \\
v_y - s n_y \\
v_z - s n_z
\end{array} \right) \\s = \frac{n_x v_x + n_y v_y + n_z v_z}{n_x^2 + n_y^2 + n_z^2}|\vec{n}|=1すなわち法線ベクトル\vec{n}が正規化されたとき、次式で表されます。
平面に投影したベクトルのxyz成分(法線ベクトル正規化時)
\vec{v'} = \left( \begin{array}{c}
v_x - s n_x \\
v_y - s n_y \\
v_z - s n_z
\end{array} \right)s = n_x v_x + n_y v_y + n_z v_z
式の証明
ベクトル\vec{v}の始点をP、終点をQとし、
\vec{v} = \vec{PQ} \tag{1}とします。
点P、点Qを平面上に投影した点をそれぞれ点P’、点Q’として、投影点の式を用いて、点P’、点Q’を求めます。
投影点を求める式
P' = P - \frac{\vec{n} \cdot \vec{AP}}{|\vec{n}|^2} \vec{n}Q' = Q - \frac{\vec{n} \cdot \vec{AQ}}{|\vec{n}|^2} \vec{n}平面に投影したベクトル\vec{v’}は、
\begin{aligned}
\vec{v'} &= \vec{P'Q'} \\
&= Q - \frac{\vec{n} \cdot \vec{AQ}}{|\vec{n}|^2} \vec{n} - \{P - \frac{\vec{n} \cdot \vec{AP}}{|\vec{n}|^2} \vec{n}\} \\
&= (Q - P) + \frac{(\vec{n} \cdot \vec{AP})\ - (\vec{n} \cdot \vec{AQ})}{|\vec{n}|^2} \vec{n} \\
&= \vec{PQ} + \frac{(\vec{n} \cdot \vec{AP})\ - (\vec{n} \cdot \vec{AQ})}{|\vec{n}|^2} \vec{n} \tag{2}
\end{aligned}ここで、
\vec{n} = \left( \begin{array}{c} n_x \\ n_y \\ n_z \end{array} \right) ,
P = \left( \begin{array}{c} p_x \\ p_y \\ p_z \end{array} \right) ,
Q = \left( \begin{array}{c} q_x \\ q_y \\ q_z \end{array} \right)とすると、
\begin{aligned}
(\vec{n} \cdot \vec{AP})\ - (\vec{n} \cdot \vec{AQ}) &= n_x (p_x - a_x) + n_y (p_y - a_y) + n_z (p_z - a_z) \\
&{} \space\space\space\space - \{n_x (q_x - a_x) + n_y (q_y - a_y) + n_z (q_z - a_z)\} \\
&= n_x (p_x - q_x) + n_y (p_y - q_y) + n_z (p_z - q_z) \\
&= \vec{n} \cdot \vec{QP} \tag{3}
\end{aligned}\begin{aligned}
\vec{v'} &= \vec{PQ} + \frac{\vec{n} \cdot \vec{QP}}{|\vec{n}|^2} \vec{n} \\
&= \vec{PQ} + \frac{\vec{n} \cdot (-\vec{PQ})}{|\vec{n}|^2} \vec{n} \\
&= \vec{v} + \frac{\vec{n} \cdot (-\vec{v})}{|\vec{n}|^2} \vec{n} \\
&= \vec{v} - \frac{\vec{n} \cdot \vec{v}}{|\vec{n}|^2} \vec{n}
\end{aligned}

