【ゲーム数学】2つのベクトルのなす角度を求める

角度を求める式

次のような、2つのベクトル\vec{a}、\vec{b}がなす角を\thetaとします。

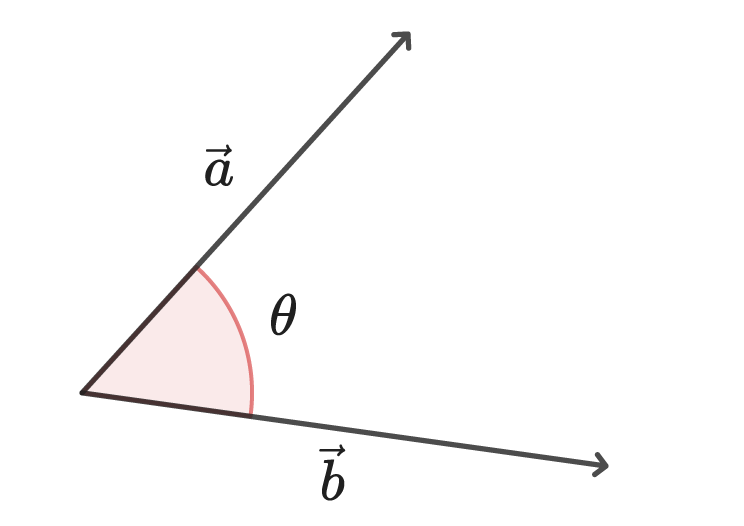
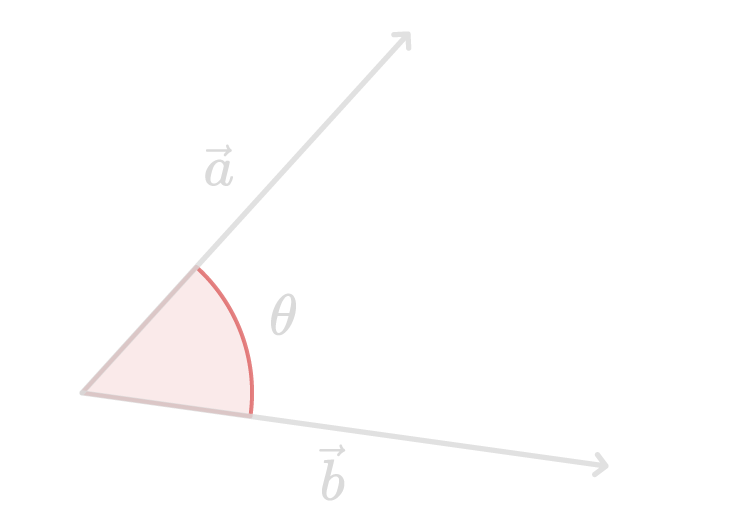
3次元ベクトル同士のなす角を求める

2つのベクトルとのなす角\thetaは、次式で求めることができます。

\theta = \arccos{\frac{ \vec{a} \cdot \vec{b} }{ |\vec{a}| |\vec{b}| }}

\arccosは逆三角関数で、アークコサインを表します。
求まる\thetaはラジアン表記で、範囲は、0 \leq \theta \leq \piです。

\vec{a}=(a_x,a_y,a_z)、\vec{b}=(b_x,b_y,b_z)とすると、次式のように表すこともできます。

\theta = \arccos{\frac{a_x b_x + a_y b_y + a_z b_z}{\sqrt{a_x^2 + a_y^2 + a_z^2}\sqrt{b_x^2 + b_y^2 + b_z^2}}}

2次元ベクトル同士のなす角を求める

2次元ベクトル同士の場合は、a_z=b_z=0として、次式のように求めることができます。

\theta = \arccos{\frac{a_x b_x + a_y b_y}{\sqrt{a_x^2 + a_y^2}\sqrt{b_x^2 + b_y^2}}}

式の証明

内積の公式を用いることで、2つのベクトルとそのなす角との関係を表現できます。

\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos \theta

両辺を|\vec{a}| |\vec{b}|で割って入れ替えると、

\cos \theta = \frac{\vec{a} \cdot \vec{b}} {|\vec{a}| |\vec{b}|}

ここで、\thetaの範囲を0 \leq \theta \leq \piとすると、逆三角関数を用いて\thetaを求めることができます。

\begin{aligned}
\theta &= \arccos (\cos \theta) \\
&= \arccos \frac{\vec{a} \cdot \vec{b}} {|\vec{a}| |\vec{b}|} \tag{1}\
\end{aligned}

内積\vec{a} \cdot \vec{b}は、ベクトルの各要素を用いて次式で表されます。

\vec{a} \cdot \vec{b} = a_x b_x + a_y b_y + a_z b_z \tag{2}

また、\vec{a}、\vec{b}の長さは、次式で表されます。

|\vec{a}| = \sqrt{a_x^2+a_y^2+a_z^2} \\
|\vec{b}| = \sqrt{b_x^2+b_y^2+b_z^2} \tag{3}

(2)(3)を(1)に代入すると、

\theta = \arccos{\frac{a_x b_x + a_y b_y + a_z b_z}{\sqrt{a_x^2 + a_y^2 + a_z^2}\sqrt{b_x^2 + b_y^2 + b_z^2}}}

2次元ベクトルの場合は、a_z=b_z=0として計算します。