目次 非表示
前提条件
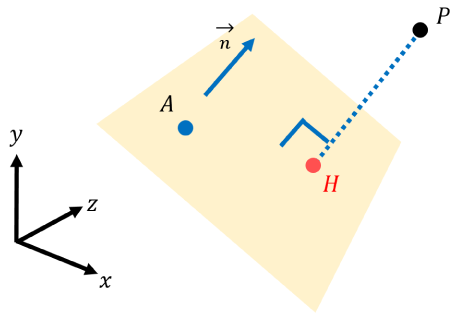
3次元空間において、法線ベクトル\vec{n}、平面を通る点Aで表現される平面に、点Pを投影したときの投影点Hの座標を求めるとします。
投影点(垂線の足)を求める式
投影点Hの座標は次式で求められます。
投影点
H = P - \frac{\vec{n} \cdot \vec{AP}}{|\vec{n}|^2} \vec{n}ただし、|\vec{n}| \neq 0
特に、|\vec{n}|=1、すなわち法線ベクトル\vec{n}が正規化された場合は、次式のようになります。
投影点(法線ベクトルが正規化された場合)
H = P - (\vec{n} \cdot \vec{AP}) \vec{n}投影点(垂線の足)のxyz座標
法線ベクトル\vec{n}、点A、点Pをそれぞれ、
\vec{n} = \left( \begin{array}{c} n_x \\ n_y \\ n_z \end{array} \right) ,
A = \left( \begin{array}{c} a_x \\ a_y \\ a_z \end{array} \right) ,
P = \left( \begin{array}{c} p_x \\ p_y \\ p_z \end{array} \right)とすると、投影点Hは次式で表現されます。
投影点のxyz座標
H = \left( \begin{array}{c}
p_x - s n_x \\
p_y - s n_y \\
p_z - s n_z
\end{array} \right)s = \frac{n_x (p_x - a_x) + n_y (p_y - a_y) + n_z (p_z - a_z)}{n_x^2 + n_y^2 + n_z^2}法線ベクトル\vec{n}が正規化された場合は、次式のようになります。
投影点のxyz座標(法線ベクトルが正規化された場合)
H = \left( \begin{array}{c}
p_x - s n_x \\
p_y - s n_y \\
p_z - s n_z
\end{array} \right)s = n_x (p_x - a_x) + n_y (p_y - a_y) + n_z (p_z - a_z)
式の証明
点APHからなる三角形に着目します。
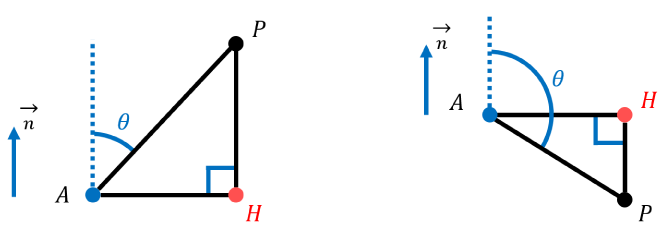
点Aを通る垂線とAPとのなす角を\thetaとすると、
\begin{aligned}
|\vec{HP}| &= ||\vec{AP}| \cos \theta| \\
&= \frac{|\vec{n}| ||\vec{AP}| \cos \theta|}{|\vec{n}|} \\
&= \frac{|\vec{n} \cdot \vec{AP}|}{|\vec{n}|}
\end{aligned}\displaystyle 0 \leq \theta \leq \frac{\pi}{2}のとき、\vec{n} \cdot \vec{AP} \geq 0より、
\begin{aligned}
\vec{HP} &= \frac{|\vec{HP}|}{|\vec{n}|} \vec{n} \\
&= \frac{\vec{n} \cdot \vec{AP}}{|\vec{n}|^2} \vec{n}
\end{aligned}\displaystyle \frac{\pi}{2} < \theta \leq \piのとき、\vec{n} \cdot \vec{AP} < 0より、
\begin{aligned}
\vec{HP} &= -\frac{|\vec{HP}|}{|\vec{n}|} \vec{n} \\
&= -\frac{-\vec{n} \cdot \vec{AP}}{|\vec{n}|^2} \vec{n} \\
&= \frac{\vec{n} \cdot \vec{AP}}{|\vec{n}|^2} \vec{n}
\end{aligned}したがって、
\begin{aligned}
H &= P - \vec{HP} \\
&= P - \frac{\vec{n} \cdot \vec{AP}}{|\vec{n}|^2} \vec{n}
\end{aligned}