ベクトルの内積について教えてほしいの。
図や計算式を用いて具体的に解説していくね。
Unityにおけるベクトル内積の基本と使い方の解説記事です。
内積は２つのベクトルから計算される値で、ベクトル同士のなす角やライティングの計算などで活用されます。
- ２つのベクトルのなす角を求める
- あるベクトルをベクトルや面に投影する
- 照射される光の強さを計算をする
ほかにも書ききれないほどの活用例が存在します。
また、内積は加算と乗算のみで求めることができ、計算が軽いという特徴があります。角度算出やライティングなどを軽い計算で実現できるのは大きなメリットと言えるでしょう。
本記事では、内積の基本的な性質を解説するとともに、活用例についてもいくつか紹介していきます。
この作品はユニティちゃんライセンス条項の元に提供されています
- Unity 2022.1.13f1
内積の定義
内積は、与えられた２つのベクトルの各要素を掛けて足した値として定義されます。２つのベクトルを\vec{a}、\vec{b}とすると、内積\vec{a} \cdot \vec{b}は次式のようになります。
\vec{a} \cdot \vec{b} = a_x b_x + a_y b_yただし、
\vec{a} = \left( \begin{array}{c} a_x \\ a_y \end{array} \right), \vec{b} = \left( \begin{array}{c} b_x \\ b_y \end{array} \right)
\vec{a} \cdot \vec{b} = a_x b_x + a_y b_y + a_z b_zただし、
\vec{a} = \left( \begin{array}{c} a_x \\ a_y \\ a_z \end{array} \right), \vec{b} = \left( \begin{array}{c} b_x \\ b_y \\ b_z \end{array} \right)得られる内積の値はスカラー量です。スクリプトからはfloat型などの値として扱われます。
また、内積はベクトルの大きさ|\vec{a}|、|\vec{b}|、両者のベクトルのなす角\thetaを用いて次式のように表現されます。 [1]
\vec{a} \cdot \vec{b} = | \vec{a} | | \vec{b} | \cos{\theta}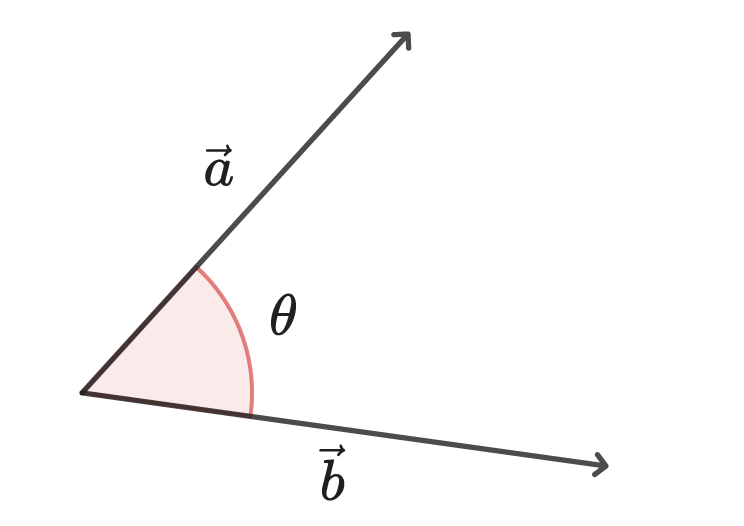
これにより、単純な加算と乗算からベクトル同士の角度関係などを調べることが可能になります。
スクリプトから内積を使う
スクリプトからは、Vector2.Dot、Vector3.Dotメソッドを用いて内積を求められます。
public static float Dot(Vector2 lhs, Vector2 rhs);引数には内積の計算対象となる2つのベクトルを指定します。
使用例は以下の通りです。
// ベクトル
Vector3 a = new Vector3(1, 2, 3);
Vector3 b = new Vector3(4, 5, 6);
// 内積を求める
float dot = Vector3.Dot(a, b);
別ベクトルへの投影
内積の便利な性質の一つとして、あるベクトルをもう一方のベクトル上に投影する計算を行えるという性質があります。
あるベクトル\vec{v}をもう一方の長さ1に正規化されたベクトル\vec{n}に投影する場合を考えます。
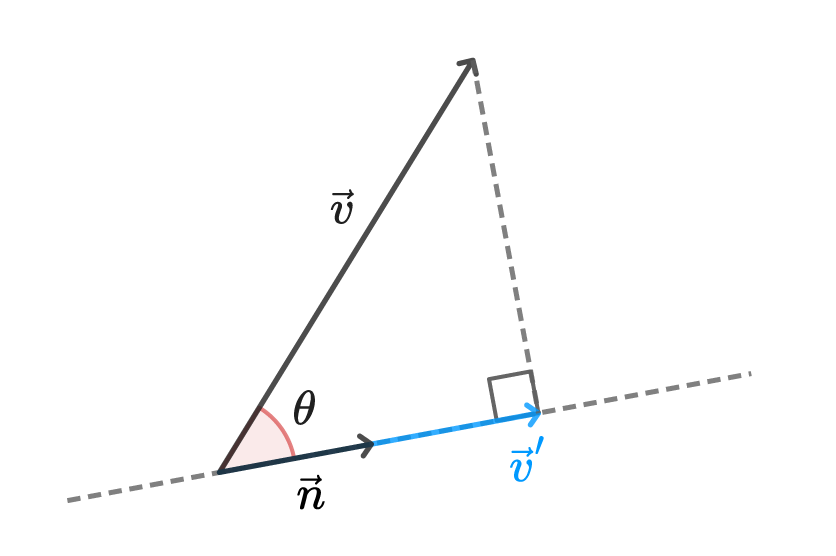
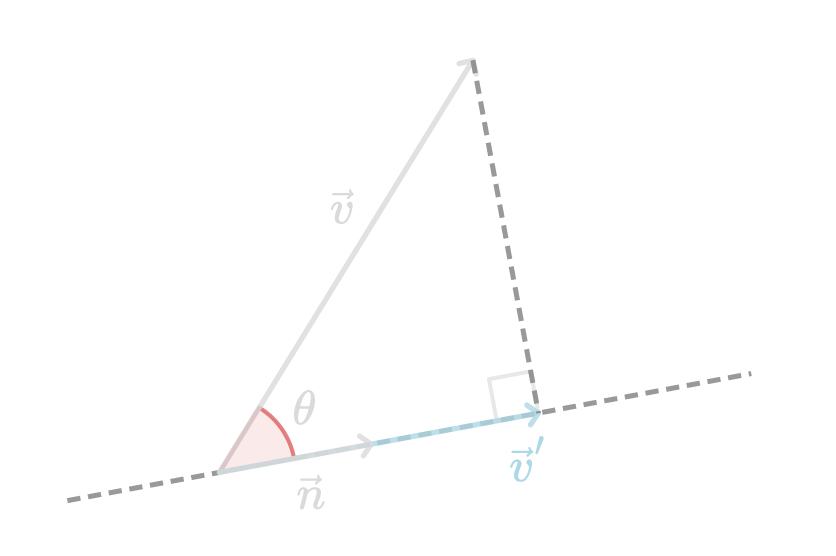
この時、|\vec{n}| = 1より、\vec{v}と\vec{n}との内積は次式のように表せます。
\vec{v} \cdot \vec{n} = |\vec{v}| \cos{\theta}右辺の|\vec{v}| \cos{\theta}を図示すると、以下のようになります。
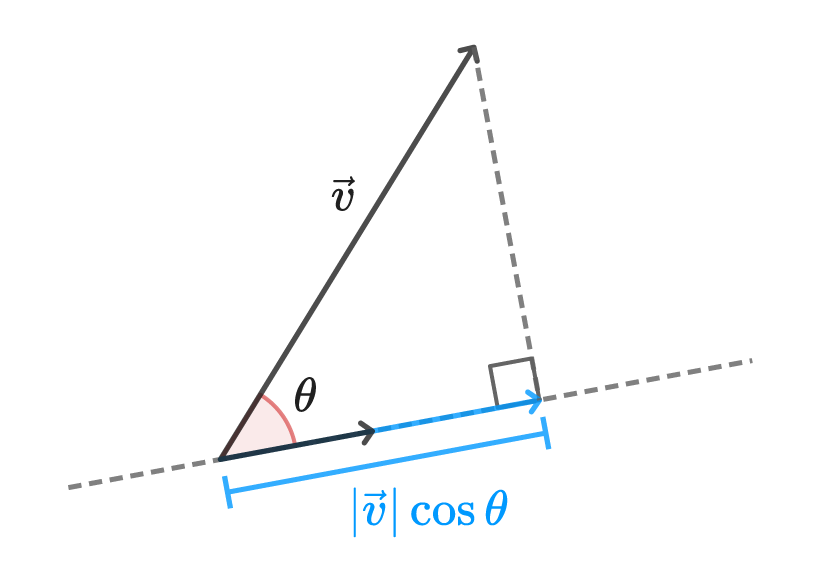
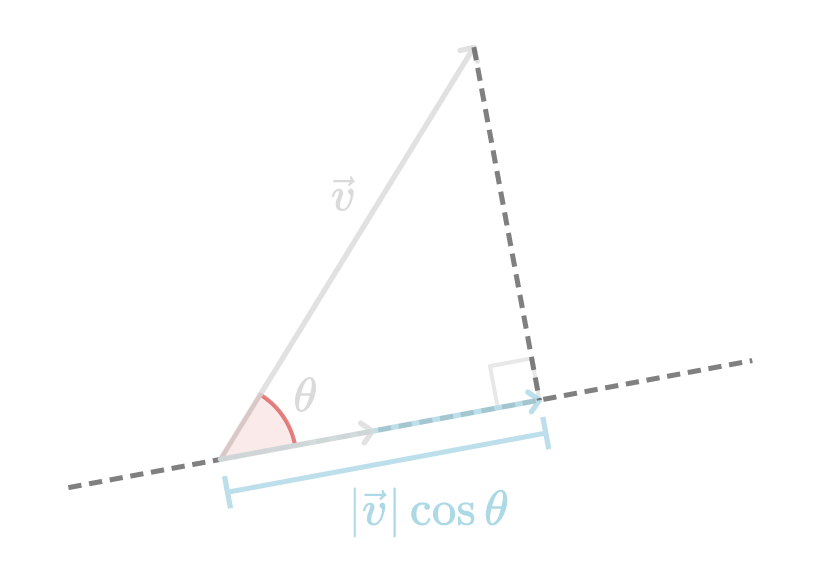
したがって、ベクトル\vec{n}に投影した位置は、内積\vec{v} \cdot \vec{n}によって求めることが可能です。
これは、ある方向におけるベクトル成分を求めたい場合などに活用できます。
ベクトル\vec{v}を\vec{n}に投影したベクトル\vec{v}’は、内積を用いて次式のように求められます。
\vec{v} ' = (\vec{v} \cdot \vec{n}) \vec{n}なお、このようなベクトル投影の計算は、Vector3.Projectメソッドでも行えます。
ベクトルのなす角を求める
2つのベクトルのなす角は、内積を用いて計算することが可能です。
2つのベクトルを\vec{a}、\vec{b}、なす角\thetaとするとき、内積の式は次のように変形できます。
\cos{\theta} = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| |\vec{b}|}最終的に、なす角\thetaはアークコサインを用いて次のように求められます。
\theta = \arccos{\frac{\vec{a} \cdot \vec{b}}{|\vec{a}| |\vec{b}|}}得られる\thetaの範囲は、0 \leq \theta \leq \piです。
角度の単位はラジアンのため、度数法として扱いたい場合は、次のように単位変換する必要があります。
\theta_{deg} = \frac{180}{\pi} \theta
このようなベクトルの角度計算は、Vector2.Angle、Vector3.Angleメソッドでも行えます。これらのメソッドは、角度計算から度数法表記への単位変換まで一括で行ってくれます。
表裏判定
内積からなす角のコサインを求められる性質を利用すると、裏表判定ができます。
例えば、ある点Pが平面のどちら側に位置しているかを判定する場合を考えます。
平面は原点Oを通り、法線ベクトル\vec{n}で定義されるものとします。
この時、\vec{OP}と\vec{n}のなす角\thetaのコサインは、内積の式から次のように表現できます。
\cos{\theta} = \frac{\vec{OP} \cdot \vec{n}}{|\vec{OP}| |\vec{n}|}また、\cos{\theta}と\thetaには次のような大小関係があります。
- 0^\circ \leq \theta < 90^\circのとき、\cos{\theta} > 0
- \theta = 90^\circのとき、\cos{\theta} = 0
- 90^\circ < \theta \leq 180^\circのとき、\cos{\theta} < 0
これにより、表裏判定は次のように内積の符号から判断できます。
- \vec{OP} \cdot \vec{n} > 0のとき、点Pは表側にある
- \vec{OP} \cdot \vec{n} = 0のとき、点Pは平面上にある
- \vec{OP} \cdot \vec{n} < 0のとき、点Pは裏側にある
Unityで提供されるPlane構造体では、このような計算で表裏判定を行うAPIが提供されています。
視線判定
前述の角度を求める計算を利用して、次のようなコーン状の視界にターゲットが存在しているかを判定できます。
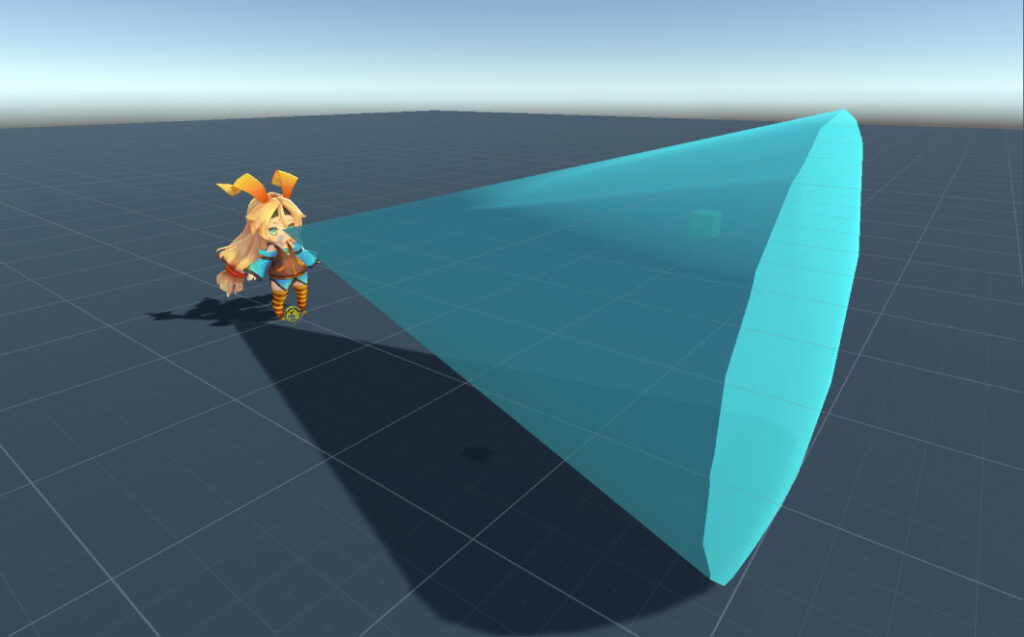
自身の位置をC、向きベクトルを\vec{d}、視野角を\theta、ターゲットの位置をPとします。
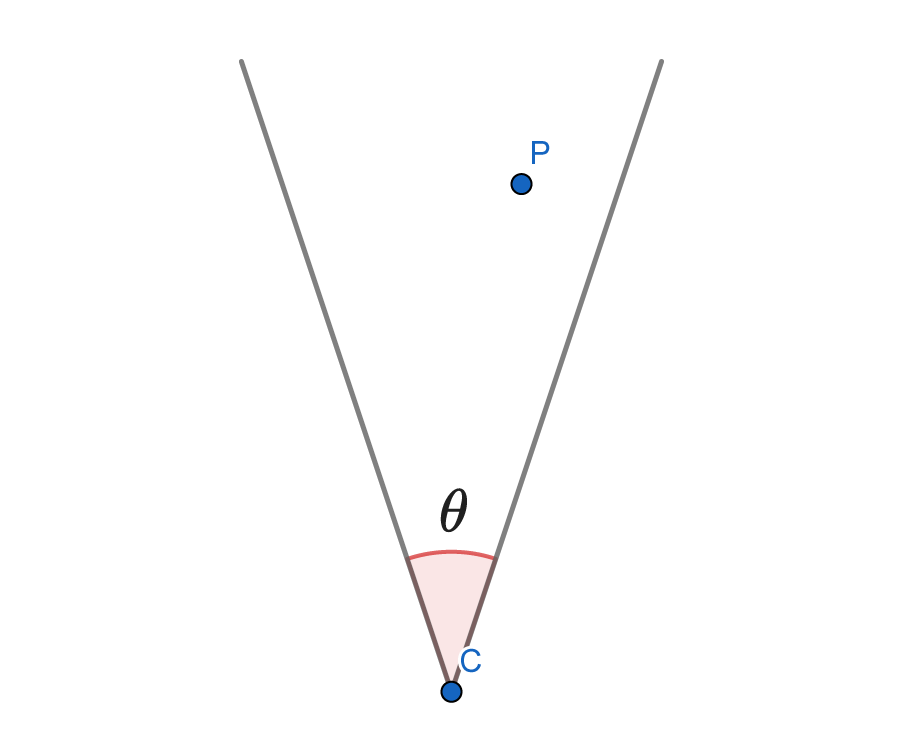
視野の範囲にターゲットがある条件は、次式のようになります。
\vec{CP} \cdot \vec{d} > |\vec{CP}| |\vec{d}| \cos{\frac{\theta}{2}}上式の不等式で判断できる理由は、0^\circ \leq \alpha < \beta \leq 180^\circのとき、\cos{\alpha} > \cos{\beta}が成り立つためです。
視線判定の実際の実装方法には以下記事で解説しておりますので、興味ある方はご覧ください。
n次元ベクトルにおける内積
ここまでは2次元、3次元ベクトルにおける内積について解説しましたが、4次元ベクトル以上においても内積を定義できます。
2つのn次元ベクトルを\bm{x}、\bm{y}とすると、内積\bm{x} \cdot \bm{y}は次式のようになります。
\bm{x} \cdot \bm{y} = x_1 y_1 + x_2 y_2 + \cdots + x_n y_nただし、
\bm{x} = \left( \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right), \bm{y} = \left( \begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_n \end{array} \right)Unityでは4次元ベクトル用のVector4.Dotメソッドが提供されています。
さいごに
内積の基本的な使い方について、いくつか例を示して解説しました。
内積を上手く活用すれば、ベクトル同士の角度や特定方向の成分、ライティングなどの計算を軽い計算で行えます。
Unityで提供するベクトル関連のAPIでは、内部的に内積が用いられているものも存在します。
本記事で紹介した以外にも様々な活用例がありますので、興味がある方は調べてみてください。
