【Unity】度数法と弧度法の違いと相互変換

度数法と弧度法の違いがよく分からないの…

どちらも角度を表す量だけど、表現方法に違いがあるの。

Unityで扱う角度には、度数法と弧度法という２つの角度表現が登場します。

角度を扱うUnity APIでは度数法が用いられることが多いですが、数学関数では弧度法が用いられます。

両者は単位が異なる角度であるため、角度の単位変換が必要になる場合もあり注意が必要です。

本記事では、度数法と弧度法の違いについて解説していきます。また、両者の相互変換方法についても触れます。

動作環境

目次非表示

度数法とは

六十分法とも呼ばれ、円周を360等分して表した角度です。30°、90度という馴染み深い表現かもしれません。

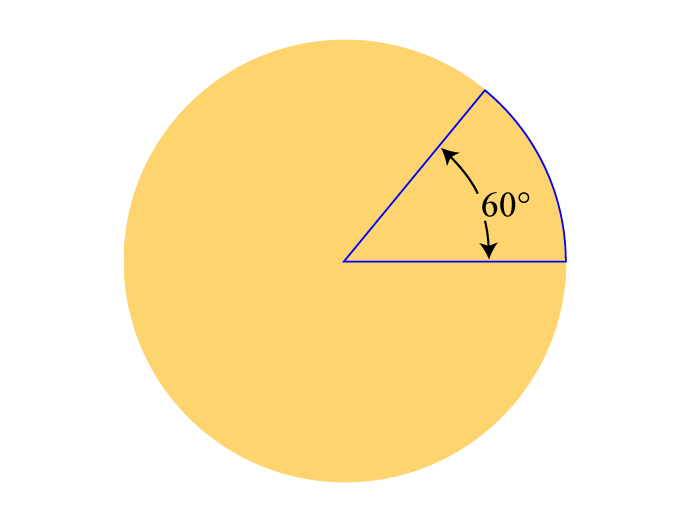
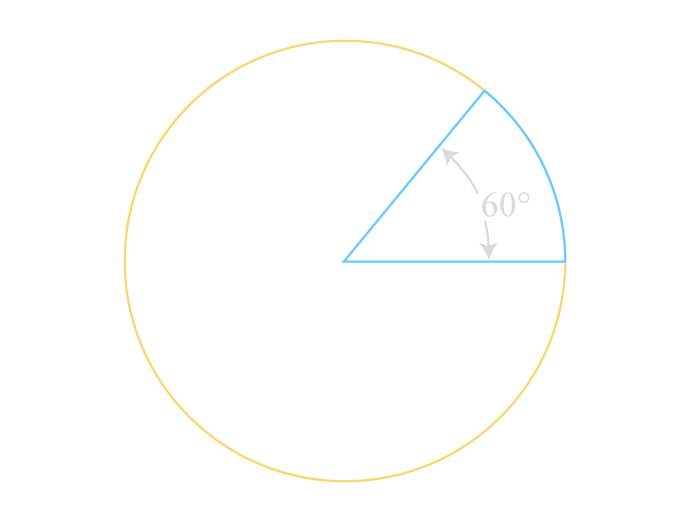
Unity APIで扱う角度の大半は度数法です。

// ベクトルのなす角
var vectorAngle = Vector3.Angle(Vector3.up, Vector3.right);

// 30°回転を表すクォータニオン
var angleAxis = Quaternion.AngleAxis(30, Vector3.up);

円弧の長さで角度を表す方法です。

下図のように、半径rの円において、円弧の長さがrとなるときの角度が1と定義されます。πラジアン、π / 4 radなどと単位表記され、単位が省略されることもあります。

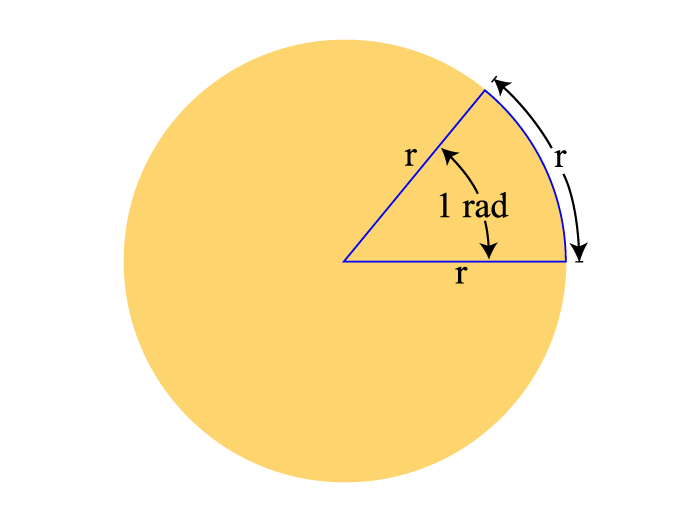
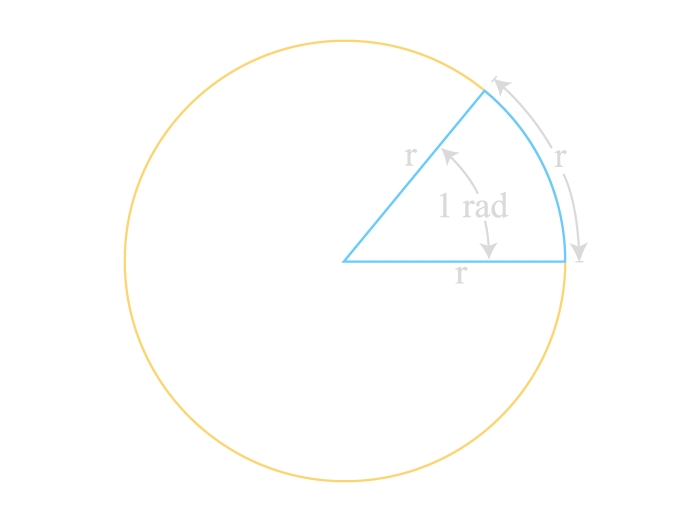
1ラジアンは、おおよそ $\dfrac{360 \degree}{2 \pi} \approx 57.3 \degree$ となります。

通常は、 $\pi$ ラジアン（ $= 180 \degree$ ）など $\pi$ 倍の値を角度として使います。

Mathf.Sinなどの数学関数では、弧度法が用いられます。

// sin(π / 2)
var sin = Mathf.Sin(Mathf.PI / 2);

// アークタンジェントから求める角度[rad]
var angleRad = Mathf.Atan2(1, 0);

度数法１週が360、弧度法は１週が2 $\pi$ であるため、両者には次のような関係があります。

度数法と弧度法の関係式

\frac{\theta_{deg}}{\theta_{rad}} = \frac{360}{2 \pi}

\theta_{rad} = \frac{\pi}{180} \theta_{deg}

$\theta_{deg}$ : 度数法表記の角度

$\theta_{rad}$ : 弧度法表記の角度

したがって、度数法の角度に $\dfrac{\pi}{180}$ という係数を掛けると弧度法の角度に変換できます。

Unityでは、この係数はMathf.Deg2Radプロパティとして提供されています。

// 度数法で90°の角度
var deg = 90;

// 弧度法に変換（π / 2になる）
var rad = Mathf.Deg2Rad * deg;

弧度法の角度に $\dfrac{180}{\pi}$ を掛けると度数法になります。

この係数はMathf.Rad2Degプロパティとして提供されています。

// 弧度法でπ
var rad = Mathf.PI;

// 度数法に変換（180°になる）
var deg = Mathf.Rad2Deg * rad;

度数法と弧度法の違い、両者の相互変換について解説しました。

Unity APIでは通常は度数法の角度を用いますが、数学関数などでは弧度法が用いられます。そのため、両者を扱う場合はどちらの角度表現なのかを混同しないように注意する必要があります。

度数法と弧度法の相互変換は、Mathf.Deg2Rad、Mathf.Rad2Degプロパティを掛ければ良いです。