【Unity】面に対象なクォータニオンを求める

ある平面に対象な回転を求めるにはどうすればいいの？

スケールによる反転ではなく、回転だけを逆向きにしたいの。

回転軸とその軸周りの回転角度を反射させれば良いわ。

ある面を境に反転したようなクォータニオンを求める方法の解説記事です。

次のように、面に対象な回転（クォータニオン）を求めることを目標とします。

これは、平面を定義する法線ベクトルから高速に計算できます。

本記事では、このように指定された面を境に反射したようなクォータニオンを求める方法を使用例とともに解説していきます。

動作環境

Unity 6000.0.32f1

目次非表示

完成系のコード
- 使用例（必要ならば）
- 実行結果
反射したクォータニオンの計算方法
拡張メソッドにするメリット
さいごに
関連記事
参考サイト様

完成系のコード

まず初めに、指定された面に反射したようなクォータニオンを算出するコードの実装例を示します。

以下はQuaternionの拡張メソッドとして実装した例です。

QuaternionExtensions.cs

using UnityEngine;

public static class QuaternionExtensions
{
    /// <summary>
    /// 指定された法線ベクトル方向で反射したクォータニオンを求める
    /// </summary>
    /// <param name="q">反射前のクォータニオン</param>
    /// <param name="normal">法線ベクトル(正規化する必要あり)</param>
    /// <returns>反射後のクォータニオン</returns>
    public static Quaternion GetReflected(this Quaternion q, Vector3 normal)
    {
        // 指定された法線ベクトルに対する反射を求める
        var num = 2 * Vector3.Dot(new Vector3(q.x, q.y, q.z), normal);

        // 反射後のクォータニオンを返す
        // 回転軸は法線ベクトルに対して反射、回転角は逆転させる
        return new Quaternion(
            num * normal.x - q.x,
            num * normal.y - q.y,
            num * normal.z - q.z,
            q.w
        );
    }
    
    /// <summary>
    /// クォータニオンを指定された法線ベクトル方向で反射する(上書き版)
    /// </summary>
    /// <param name="q">反射前のクォータニオン</param>
    /// <param name="normal">法線ベクトル(正規化する必要あり)</param>
    public static void Reflect(this ref Quaternion q, Vector3 normal)
    {
        q = q.GetReflected(normal);
    }
}

上記をQuaternionExtensions.csなどという名前でUnityプロジェクトに保存すると、Quaternionの拡張メソッドとしてQuaternion.GetReflected、Quaternion.Reflectメソッドが使用可能になります。

使用例（必要ならば）

前述の拡張メソッドの使用例です。

指定されたオブジェクトの回転（rotation）を入力として、反射したクォータニオンを計算し、別オブジェクトの回転に指定しています。

UseExample.cs

using UnityEngine;

public class UseExample : MonoBehaviour
{
    // 入力元のクォータニオンとして使用するオブジェクト
    [SerializeField] private Transform _source;
    
    // 反射後のクォータニオンを適用するオブジェクト
    [SerializeField] private Transform _target;

    // 反射する面の法線ベクトル
    [SerializeField] private Vector3 _normal = Vector3.right;

    private void Update()
    {
        // 元の回転を取得
        var sourceRotation = _source.rotation;
        
        // normalで指定された面に反射した回転を取得
        var reflectedRotation = sourceRotation.GetReflected(_normal.normalized);
        
        // 反射した回転を_targetに適用
        _target.rotation = reflectedRotation;
    }
}

上記をUseExample.csという名前でUnityプロジェクトに保存しておきます。

これを適当なゲームオブジェクトに追加し、以下項目を設定すればリアルタイムに計算前と計算後の結果を確認することができるようになります。

Source – 計算前のクォータニオンとして使用するオブジェクト
Target – 計算後の結果を反映するオブジェクト
Normal – 面を定義する法線ベクトル

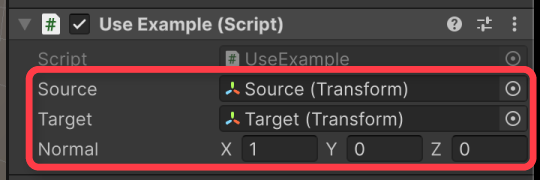
実行結果

Sourceに指定したオブジェクトを回転させると、出力先のTargetオブジェクトがNormalで定義した面を対象に回転していることを確認できます。

反射したクォータニオンの計算方法

ここから先は、前述の処理でクォータニオンの反射が計算できる理由について解説していきます。

本章は計算式の証明がメインとなるため、不要な方は次の章まで読み飛ばしていただいて問題ありません。

注意

本記事では、クォータニオンを用いた数式の説明および導出過程のみ示すものとし、クォータニオン自体の基礎的な解説は省略いたします。

計算式

計算元となる入力クォータニオンを $\bm{q}$ 、面を定義する法線ベクトルを $\bm{n}$ とすると、 $\bm{q}$ を $\bm{n}$ 方向で反射させたクォータニオン $\bm{q^{\prime}}$ は次式のようになります。

反射したクォータニオンを求める式

\bm{q^{\prime}} = \left( \begin{array}{c} 2 (\bm{v} \cdot \bm{n}) n_x - q_x \\ 2 (\bm{v} \cdot \bm{n}) n_y - q_y \\ 2 (\bm{v} \cdot \bm{n}) n_z - q_z \\ q_w \end{array} \right)

ただし、

\bm{q} = \left( \begin{array}{c} q_x \\ q_y \\ q_z \\ q_w \end{array} \right), \bm{n} = \left( \begin{array}{c} n_x \\ n_y \\ n_z \end{array} \right) , \bm{v} = \left( \begin{array}{c} q_x \\ q_y \\ q_z \end{array} \right)

\|\bm{n}\| = 1

計算式の導出過程

得られるクォータニオン $\bm{q^{\prime}}$ は、 $\bm{q}$ に対して次の操作を行った結果となります。

回転軸を面を定義する法線ベクトル $\bm{n}$ に対して反射させる
回転軸回りの回転角度の符号を反転させる

クォータニオン自体は、回転軸 $\bm{a}$ と回転角度 $\theta$ から次式のように求められます。

\bm{q} = \left( \begin{array}{c} a_x \displaystyle\sin{\frac{\theta}{2}} \\ \\ a_y \displaystyle\sin{\frac{\theta}{2}}\\ \\ a_z \displaystyle\sin{ \frac{\theta}{2}} \\ \\ \displaystyle\cos{ \frac{\theta}{2}}\end{array} \right)

ただし、

\bm{a} = \left( \begin{array}{c} a_x \\ a_y \\ a_z \end{array} \right)

この時、反射した回転軸 $\bm{a^{\prime}}$ 、符号反転した回転角度 $\theta^{\prime}$ は次式のようになります。

\bm{a^{\prime}} = \bm{a} - 2 (\bm{a} \cdot \bm{n}) \bm{n}

\theta^{\prime} = -\theta

反射ベクトルを求める際、法線ベクトルとの内積を2倍して引く理由は、1倍でちょうど面に投影したベクトルとなり、2倍すると面と反対方向に移動できるためです。

メモ

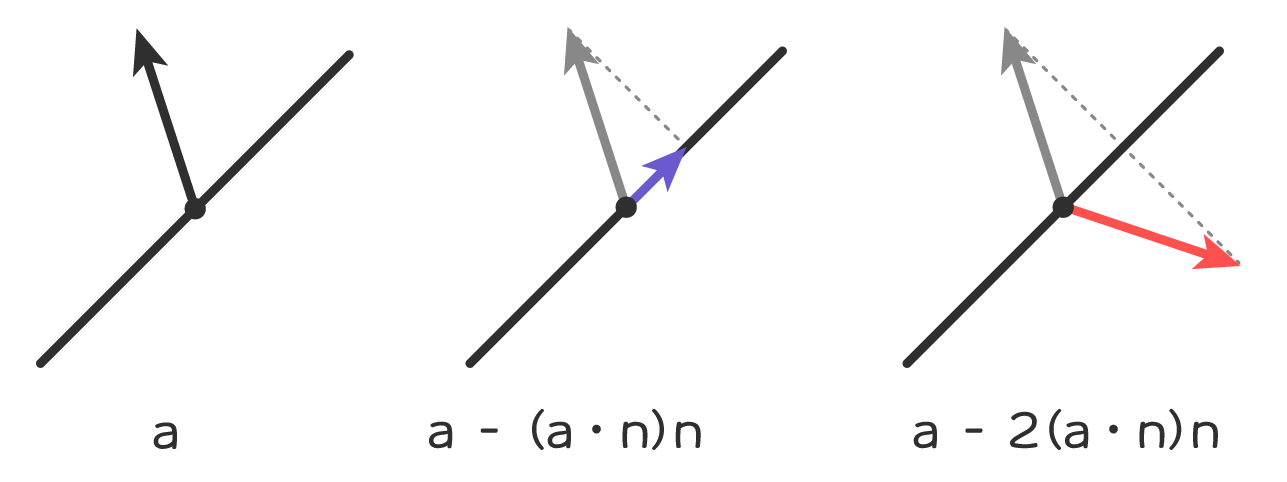
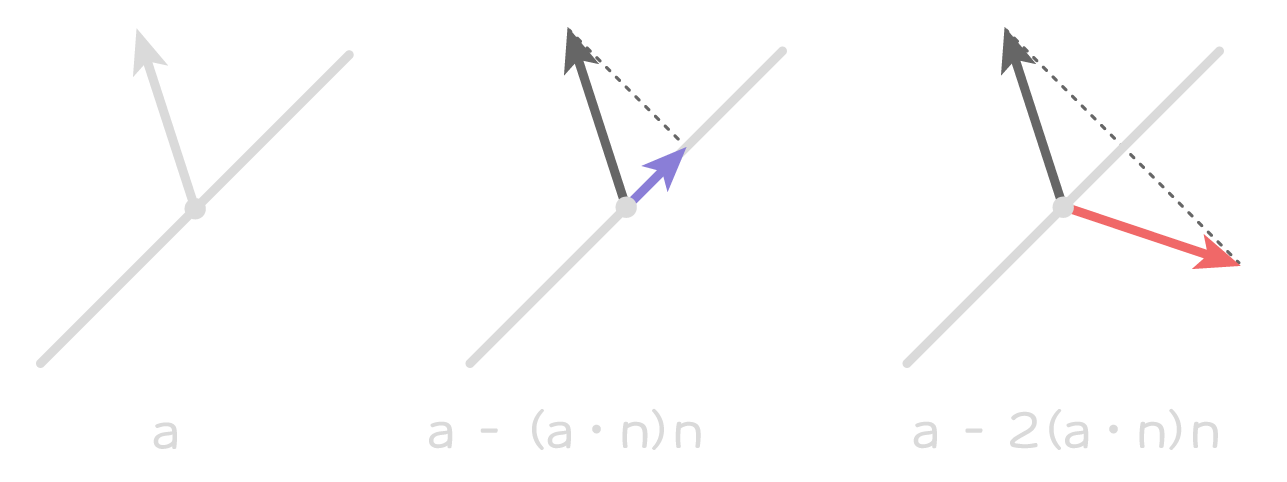
このような反射ベクトルは、Vector2.Reflect、Vector3.Reflectメソッドで計算することも可能です。

Vector3 inDirection, inNormal;

・・・（中略）・・・

// 反射ベクトルを求める
var result = Vector3.Reflect(inDirection, inNormal);

内部的には同様の計算で求めています。

参考：Vector2-Reflect – Unity スクリプトリファレンス

参考：Vector3-Reflect – Unity スクリプトリファレンス

【Unity】面で反射したベクトルを求める

ある平面で反射したベクトルを求めたい場合、Vector3.Reflectメソッドを用いれば簡単に取得できます。２次元版のVector2.Reflectメソッドも用意されています。本記事で、実際の使用例を示しながら、こ…

2021年11月1日

クォータニオン $\bm{q}$ を法線ベクトル $\bm{n}$ 方向で反射したクォータニオン $\bm{q^{\prime}}$ を

\bm{q^{\prime}} = \left( \begin{array}{c} a_x^{\prime} \displaystyle\sin{\frac{\theta^{\prime}}{2}} \\ \\ a_y^{\prime} \displaystyle\sin{\frac{\theta^{\prime}}{2}}\\ \\ a_z^{\prime} \displaystyle\sin{ \frac{\theta^{\prime}}{2}} \\ \\ \displaystyle\cos{ \frac{\theta^{\prime}}{2}}\end{array} \right)

とすると、次式のように変形できます。

\bm{q^{\prime}} = \left( \begin{array}{c} \{a_x - 2(\bm{a} \cdot \bm{n}) n_x\} \displaystyle\sin{\frac{-\theta}{2}} \\ \\ \{a_y - 2(\bm{a} \cdot \bm{n}) n_y\} \displaystyle\sin{\frac{-\theta}{2}}\\ \\ \{a_z - 2(\bm{a} \cdot \bm{n}) n_z\} \displaystyle\sin{\frac{-\theta}{2}} \\ \\ \displaystyle\cos{ \frac{-\theta}{2}}\end{array} \right)

ここで、

\sin({-\theta}) = -\sin{\theta}, \cos({-\theta}) = \cos{\theta}

なる性質を用いると、次式のようになります。

\bm{q^{\prime}} = \left( \begin{array}{c} -\{a_x - 2(\bm{a} \cdot \bm{n}) n_x\} \displaystyle\sin{\frac{\theta}{2}} \\ \\ -\{a_y - 2(\bm{a} \cdot \bm{n}) n_y\} \displaystyle\sin{\frac{\theta}{2}}\\ \\ -\{a_z - 2(\bm{a} \cdot \bm{n}) n_z\} \displaystyle\sin{\frac{\theta}{2}} \\ \\ \displaystyle\cos{ \frac{\theta}{2}}\end{array} \right)

ここで、

q_x = a_x \displaystyle\sin{\frac{\theta}{2}}, q_y = a_y \displaystyle\sin{\frac{\theta}{2}}

q_z = a_z \displaystyle\sin{\frac{\theta}{2}}, q_w = \displaystyle\cos{\frac{\theta}{2}}

であるため、これらを用いて $\bm{q^{\prime}}$ は次式のように表現できます。

\bm{q^{\prime}} = \left( \begin{array}{c} -q_x + 2(\bm{a} \cdot \bm{n}) n_x \displaystyle\sin{\frac{\theta}{2}} \\ \\ -q_y + 2(\bm{a} \cdot \bm{n}) n_y \displaystyle\sin{\frac{\theta}{2}} \\ \\ -q_z + 2(\bm{a} \cdot \bm{n}) n_z \displaystyle\sin{\frac{\theta}{2}} \\ \\ q_w \end{array} \right)

また、

\bm{v} = \left( \begin{array}{c} q_x \\ q_y \\ q_z \end{array} \right) = \left( \begin{array}{c} a_x \displaystyle\sin{\frac{\theta}{2}} \\\\ a_y \displaystyle\sin{\frac{\theta}{2}} \\\\ a_z \displaystyle\sin{\frac{\theta}{2}} \end{array} \right)

とすると、

(\bm{a} \cdot \bm{n}) \displaystyle\sin{\frac{\theta}{2}} = \bm{v} \cdot \bm{n}

と置き換えられるため、最終的な $\bm{q^{\prime}}$ は次式のように変形できます。

\bm{q^{\prime}} = \left( \begin{array}{c} 2(\bm{v} \cdot \bm{n}) n_x - q_x \\ 2(\bm{v} \cdot \bm{n}) n_y - q_y \\ 2(\bm{v} \cdot \bm{n}) n_z - q_z \\ q_w \end{array} \right)

ノルムの変化

ここまで面で反射したクォータニオンを求める導出過程を解説しましたが、ノルムがどう変化するか気になる方がいるかもしれません。

そこで、計算前のクォータニオン $\bm{q}$ と計算後のクォータニオン $\bm{q^{\prime}}$ のノルムの関係についても触れておきます。

クォータニオン $\bm{q}$ 、 $\bm{q^{\prime}}$ のノルムをそれぞれ $\|\bm{q}\|$ 、 $\|\bm{q^{\prime}}\|$ とすると、次式のように各要素の総和の平方根として表されます。

\|\bm{q}\| = \sqrt{q_x^2 + q_y^2 + q_z^2 + q_w^2}

\|\bm{q^{\prime}}\| = \sqrt{q_x^{\prime2} + q_y^{\prime2} + q_z^{\prime2} + q_w^{\prime2}}

ここで、

\bm{q^{\prime}} = \left( \begin{array}{c} q_x^{\prime} \\ q_y^{\prime} \\ q_z^{\prime} \\ q_w^{\prime} \end{array} \right) = \left( \begin{array}{c} 2(\bm{v} \cdot \bm{n}) n_x - q_x \\ 2(\bm{v} \cdot \bm{n}) n_y - q_y \\ 2(\bm{v} \cdot \bm{n}) n_z - q_z \\ q_w \end{array} \right)

であるため、ノルム $\|\bm{q^{\prime}}\|$ は次式のように変形できます。

\begin{aligned} \|\bm{q^{\prime}}\| &= \sqrt{ (2(\bm{v} \cdot \bm{n}) n_x - q_x)^2 + (2(\bm{v} \cdot \bm{n}) n_y - q_y)^2 + (2(\bm{v} \cdot \bm{n}) n_z - q_z)^2 + q_w^2 } \\ &= \sqrt{4 (\bm{v} \cdot \bm{n})^2 ( n_x^2 + n_y^2 + n_x^z ) - 4 (\bm{v} \cdot \bm{n})(n_x q_x + n_y q_y + n_z q_z) + q_x^2 + q_y^2 + q_z^2 + q_w^2} \\ \end{aligned}

ここで法線ベクトル $\bm{n}$ の長さは1としているため、次式の関係が成り立ちます。

\|\bm{n}\|^2 = n_x^2 + n_y^2 + n_z^2 = 1

また、内積 $\bm{v} \cdot \bm{n}$ は

\bm{v} \cdot \bm{n} = q_x n_x + q_y n_y + q_z n_z

であることから、最終的に計算後のノルム $\|\bm{q^{\prime}}\|$ は次式のようになります。

\begin{aligned} \|\bm{q^{\prime}}\| &= \sqrt{ 4 (\bm{v} \cdot \bm{n})^2 - 4 (\bm{v} \cdot \bm{n})(\bm{v} \cdot \bm{n}) + q_x^2 + q_y^2 + q_z^2 + q_w^2 } \\ &= \sqrt{ 4 (\bm{v} \cdot \bm{n})^2 - 4 (\bm{v} \cdot \bm{n})^2 + q_x^2 + q_y^2 + q_z^2 + q_w^2 } \\ &= \sqrt{q_x^2 + q_y^2 + q_z^2 + q_w^2} \\ &= \|\bm{q}\| \end{aligned}

これは、ノルム $\|\bm{q}\|$ と $\|\bm{q^{\prime}}\|$ は等しい、すなわちクォータニオンの反射計算でノルムが変化しないことを意味します。

ただし、計算誤差によってノルムに誤差が蓄積する可能性はあるため、それが不都合になる場合はノルムが1になるように正規化しておくとよいでしょう。

拡張メソッドにするメリット

実装例では、Quaternionの拡張メソッドとして反射ベクトルを求めるメソッドを定義しましたが、拡張メソッド化することで、Quaternionのメソッドであるかのように使用することができます。

Quaternion rotation;
Vector3 normal;

・・・（中略）・・・

// normalで指定された面に反射した回転を取得
var reflectedRotation = rotation.GetReflected(normal);

// rotation自体に反映
rotation.Reflect(normal);