【Unity】クォータニオンのLerpとSlerpの挙動の違い

こじゃらこじゃら

クォータニオンのLerpとSlerpって何が違うの？

両者の結果の違いや処理負荷についても知りたいの。

このはこのは

Lerpは線形補間、Slerpは球面線形補間という違いがあるわ。

Lerpは計算結果が軽め、Slerpは綺麗な補間ができるという違いがあるわ。

Unityのクォータニオンがサポートしている2種類の補間方式であるLerpとSlerpの挙動の違いについての解説記事です。

両者とも2つのクォータニオンを補間した結果を求めるメソッドですが、Lerpは線形補間、Slerpは球面線形補間という計算方法で補間するといった違いがあります。

参考：Quaternion-Lerp – Unity スクリプトリファレンス

参考：Quaternion-Slerp – Unity スクリプトリファレンス

一般的に、Lerpは計算が軽い分、回転角度が大きいと不均一な速度になる、Slerpは均一な速度で回転するが、計算はLerpと比較して重いといった特徴があります。

LerpとSlerpの違い
  • Quaternion.Lerp
    • 2つのクォータニオンの各要素を線形補間し、ノルムが1になるように正規化
    • Slerpと比較して計算が軽い
    • 角度が遠いクォータニオン同士の場合は、回転速度が均一にならない
    • 角度が近いクォータニオン同士の場合は、回転速度はほぼ均一になる
  • Quaternion.Slerp
    • 2つのクォータニオンの各要素を球面線形補間する
    • 内部的にSin関数を使うため、Lerpと比較して計算は重い
    • 角度が遠いクォータニオン同士でも、回転速度が均一になるような補間が可能

また、Unity公式のMathematicsパッケージが提供するquaternion構造体にも同様のメソッドがあります。

Mathematicsパッケージのquaternionの補間メソッド
  • quaternion.nlerp – 線形補間
  • quaternion.slerp – 球面線形補間

quaternion.nlerpメソッドはQuaternion.Lerpメソッドと名前が違いますが、基本的な挙動はほぼ一緒です。

参考：Method nlerp | Mathematics | 1.3.2

本記事では、クォータニオンのLerpおよびSlerpメソッドのそれぞれの仕様や挙動の違いについて解説していきます。

また、両者の処理負荷の比較や内部の計算式についても触れます。

動作環境
  • Unity 6000.0.32f1

スポンサーリンク

目次 非表示

クォータニオンのLerpおよびSlerpメソッドの仕様と挙動

まず初めに、両者のメソッドの仕様について触れておきます。

Quaternion.Lerp／quaternion.nlerp

与えられた2つのクォータニオンを与えられた割合で線形補間するstaticメソッドです。

Quaternion.Lerpメソッド（tを0～1の範囲にクランプ）

public static Quaternion Lerp(Quaternion a, Quaternion b, float t);

Mathematics.quaternion.nlerpメソッド（tはクランプしない）

public static quaternion nlerp(quaternion q1, quaternion q2, float t)

第1、第2引数に補間に使用する2つのクォータニオン、第3引数tには0〜1の範囲で割合を指定します。

Quaternion.Lerpメソッドはtを0～1の範囲にクランプしますが、quaternion.nlerpはクランプされません。

Quaternion.Lerpを使いたいがtをクランプしたくない場合は、Quaternion.LerpUnclampedメソッドを使用します。

Quaternion.LerpUnclampedメソッド（tはクランプしない）

public static Quaternion LerpUnclamped(Quaternion a, Quaternion b, float t);

戻り値として、線形補間されたクォータニオンが返されます。クォータニオンのノルムはいずれも1に正規化されます。

参考：Quaternion-Lerp – Unity スクリプトリファレンス

参考：Method nlerp | Mathematics | 1.3.2

参考：Quaternion-LerpUnclamped – Unity スクリプトリファレンス

Quaternion.Slerp／quaternion.slerp

2つのクォータニオンを与えられた割合で球面線形補間するstaticメソッドです。Lerp（nlerp）との違いは線形補間が球面線形補間に変わった点です。

Quaternion.Slerpメソッド（tを0～1の範囲にクランプ）

public static Quaternion Slerp(Quaternion a, Quaternion b, float t);

Mathematics.quaternion.slerpメソッド（tはクランプしない）

public static quaternion slerp(quaternion q1, quaternion q2, float t)

引数の形式はLerpメソッドと一緒です。Quaternion.Slerpメソッドはtがクランプされるので、されたくない場合はQuaternion.SlerpUnclampedメソッドを使います。

Quaternion.SlerpUnclampedメソッド（tはクランプしない）

public static Quaternion SlerpUnclamped(Quaternion a, Quaternion b, float t);

戻り値は、球面線形補間されたクォータニオンです。

参考：Quaternion-Slerp – Unity スクリプトリファレンス

参考：Method slerp | Mathematics | 1.3.2

参考：Quaternion-SlerpUnclamped – Unity スクリプトリファレンス

両者の比較用スクリプト

以下、Lerp（線形補間）とSlerp（球面線形補間）の挙動を比較するためのサンプルスクリプトです。

QuaternionLerpSlerpExample.cs
using UnityEngine;

public class QuaternionLerpSlerpExample : MonoBehaviour
{
    // 補間元のクォータニオンに使用するオブジェクト
    [SerializeField] private Transform _source1;
    [SerializeField] private Transform _source2;

    // 補間先のオブジェクト(Lerp)
    [SerializeField] private Transform _lerpTarget;

    // 補間先のオブジェクト(Slerp)
    [SerializeField] private Transform _slerpTarget;

    // 補間の割合(0～1)
    [SerializeField, Range(0, 1)] private float _t = 0.5f;
    
    // 割合を0～1の範囲で往復させるか
    [SerializeField] private bool _pingPong = true;

    private void Update()
    {
        if (_pingPong)
        {
            // 割合tを0～1の範囲で往復させる
            _t = Mathf.PingPong(Time.time, 1);
        }
        
        var q1 = _source1.rotation;
        var q2 = _source2.rotation;

        // 線形補間(Lerp)
        var lerp = Quaternion.Lerp(q1, q2, _t);
        _lerpTarget.rotation = lerp;

        // 球面線形補間(Slerp)
        var slerp = Quaternion.Slerp(q1, q2, _t);
        _slerpTarget.rotation = slerp;
    }
}

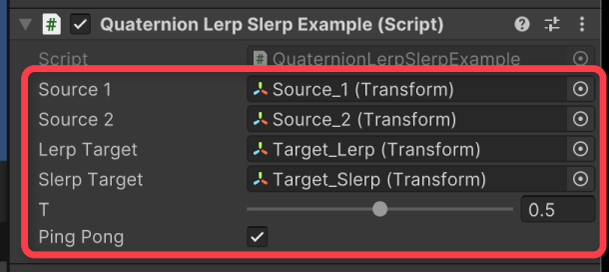
上記をQuaternionLerpSlerpExample.csという名前でUnityプロジェクトに保存し、適当なゲームオブジェクトに追加し、以下設定を行えば機能します。

  • Source 1 – 補間元のクォータニオンに使用するオブジェクト1
  • Source 2 – 補間元のクォータニオンに使用するオブジェクト2
  • Lerp Target – 線形補間（Lerp）の結果を反映するオブジェクト
  • SlerpTarget – 球面線形補間（Slerp）の結果を反映するオブジェクト
  • T – 補間の割合
  • Ping Pong – 割合tを自動で往復させるかどうか

実行結果

補間元となる2つのオブジェクトの回転（rotation）が反映先オブジェクトの回転に反映されていることが確認できました。

例では分かりやすさのため、オブジェクトのローカル軸を表示させています。

見た目上僅かな差ですが、Lerpでは開始と終了時の速度が少し遅く、中盤辺り（割合t=0.5付近）の回転速度が速くなっています。一方で、Slerpは常に均一な速さで回転しています。

クォータニオン同士の角度の大きさによる出力結果の比較

線形補間（Lerp）は2つのクォータニオンの角度が離れている場合は不均一な速さになりますが、角度が近い場合はほぼ均一な速さになります。

角度が離れている場合
角度が近い場合

球面線形補間（Slerp）は角度が近くても離れても常に均一な速さが保たれていることが確認できます。

処理負荷の比較

ここまでLerpとSlerpの計算結果を比較してきましたが、ここからは処理負荷について検証してみます。

検証用スクリプト

以下、LerpとSlerpの処理負荷を計測し、結果をログ出力する例です。

LerpとSlerpそれぞれ100万回実行し、その処理時間をミリ秒単位で出力します。

CheckLerpSlerpPerformanceExample.cs
using System.Diagnostics;
using UnityEngine;

/// <summary>
/// LerpとSlerpのパフォーマンスを比較する
/// </summary>
public class CheckLerpSlerpPerformanceExample : MonoBehaviour
{
    private void Start()
    {
        // 計測回数(100万回)
        const int iteration = 1000000;
        
        // 入力情報
        var q1List = new Quaternion[iteration];
        var q2List = new Quaternion[iteration];
        var tList = new float[iteration];

        // ランダムな値を入力情報に設定
        for (var i = 0; i < iteration; i++)
        {
            q1List[i] = Random.rotation;
            q2List[i] = Random.rotation;
            tList[i] = Random.value;
        }
        
        // 線形補間(Lerp)の処理時間計測
        var stopwatchLerp = Stopwatch.StartNew();
        for (var i = 0; i < iteration; i++)
        {
            var lerp = Quaternion.Lerp(q1List[i], q2List[i], tList[i]);
        }
        stopwatchLerp.Stop();
        
        // 球面線形補間(Slerp)の処理時間計測
        var stopwatchSlerp = Stopwatch.StartNew();
        for (var i = 0; i < iteration; i++)
        {
            var slerp = Quaternion.Slerp(q1List[i], q2List[i], tList[i]);
        }
        stopwatchSlerp.Stop();
        
        // 結果を表示
        UnityEngine.Debug.Log($"Lerp: {stopwatchLerp.Elapsed.TotalMilliseconds:F3} ms");
        UnityEngine.Debug.Log($"Slerp: {stopwatchSlerp.Elapsed.TotalMilliseconds:F3} ms");
    }
}

上記をCheckLerpSlerpPerformanceExample.csという名前でUnityプロジェクトに保存し、適当なゲームオブジェクトに追加すると機能します。

実行結果

以下の結果となりました。いずれもエディタ環境での計測結果となります。

Quaternion.Lerp()Quaternion.Slerp()
処理時間[ms]23.246650.3884

SlerpはLerpと比較しておおよそ2倍少々の処理時間がかかる結果となりました。

上記の結果から、LerpよりSlerpのほうが処理コストは高いことが確認できます。Lerpは四則演算および平方根の計算で済みますが、SlerpはSin関数を内部的に呼び出しているため、ここで差が生じています。

補間の計算式

次に、LerpとSlerpがどのような計算式で補間しているかを解説していきます。

なお、執筆の際は、Mathematicsパッケージの内部実装を参考にさせていただきました。

注意

本章で示す数式は厳密に実装に一致しているものではなく、あくまで大まかな処理から推測・整理された式となることにご注意ください。

線形補間（Lerp）

次式のような計算を行っています。

\bm{q_{lerp}} = \frac{\bm{q_1} + t(\bm{q_2} - \bm{q_1})}{\|\bm{q_1} + t(\bm{q_2} - \bm{q_1})\|}

ただし、

\bm{q_1}, \bm{q_2} : 補間元のクォータニオン

0 \le t \le 1

線形補間では、そのまま計算するとノルムが1以外に変化してしまうので、1になるようにノルムで割って正規化しています。

クォータニオンのノルムは、各要素の二乗和の平方根として計算されます。

\|\bm{q}\| = \sqrt{x^2+y^2+z^2+w^2}

ただし、

\bm{q} = \left( \begin{array}{c} x \\ y \\ z \\ w \end{array} \right)

球面線形補間（Slerp）

次式のように計算されます。

\bm{q_{slerp}} = \frac{\sin{(1-t)\theta}}{\sin{\theta}} \bm{q_1} + \frac{\sin{t\theta}}{\sin{\theta}} \bm{q_2}
\theta = \arccos{(\bm{q_1} \cdot \bm{q_2})}

ただし、

0 \le t \le 1

\|\bm{q_1}\| = \|\bm{q_2}\| = 1

この数式から分かるように、Sin関数に相当する計算を3回計算する必要があるため、処理負荷増大に繋がっています。

また、クォータニオンの球面線形補間の式は、3次元ベクトルの球面線形補間と数式がほぼ一致しており、超球面を移動するような補間処理が行われます。これによってどの角度でも均一な速さで回転するような挙動が実現できます。

メモ

3次元ベクトルの球面線形補間は次式の通りです。

\bm{v} = \frac{\sin{(1-t)\theta}}{\sin{\theta}} \bm{v_1} + \frac{\sin{t\theta}}{\sin{\theta}} \bm{v_2}
\theta = \arccos(\bm{v_1} \cdot \bm{v_2})

ただし、

\bm{v}、\bm{v_1}、\bm{v_2}は3次元ベクトル

\|\bm{v_1}\| = \|\bm{v_2}\| = 1

Mathematics.quaternion.slerpメソッドの内部処理

Mathematics.quaternion構造体のslerpメソッドでは、クォータニオンの内積が必ず0以上になるような計算処理が行われています。

quaternion.slerpメソッドの抜粋コード

float dt = dot(q1, q2);
if (dt < 0.0f)
{
    dt = -dt;
    q2.value = -q2.value;
}

このような符号反転処理が成り立つ理由は、クォータニオンの全要素の符号を反転したクォータニオン-\bm{q}は同じ回転を表す性質があるためです。

R(-\bm{q}) = R(\bm{q})

また、内積が負だった場合、片方のクォータニオンの符号を反転させて正にすることで、角度の近い道のりで回転させることが可能です。

また、クォータニオン同士の内積の値が1に非常に近い場合、内部的にquaternion.nlerpメソッドの結果を返しています。すなわち線形補間するように条件分岐されています。

quaternion.slerpメソッドの抜粋コード

if (dt < 0.9995f)
{
    float angle = acos(dt);
    float s = rsqrt(1.0f - dt * dt);    // 1.0f / sin(angle)
    float w1 = sin(angle * (1.0f - t)) * s;
    float w2 = sin(angle * t) * s;
    return quaternion(q1.value * w1 + q2.value * w2);
}
else
{
    // if the angle is small, use linear interpolation
    return nlerp(q1, q2, t);
}

内積が1に非常に近い場合は、クォータニオン同士の角度が0に近いため、線形補間でも球面線形補間と変わらずほぼ均一な速度の補間結果が得られます。

さいごに

クォータニオンの線形補間（Lerp）と球面線形補間（Slerp）は、内部的な補間計算式が異なる違いがあります。

2つのクォータニオンの角度が非常に近い場合は両者の結果にほぼ差異が見られませんが、角度が離れるほど線形補間のほうは速度が不均一になってしまう違いが生じます。

球面線形補間のほうが綺麗な結果が得られますが、処理コストは線形補間より大きいため、これらの特性を理解して使い分けると良いでしょう。

関連記事

参考サイト様

スポンサーリンク

前の記事

【Unity】面に対象なクォータニオンを求める