Vector3.Lerp()とVector3.Slerp()はどう違うの？どうやって使うの？
どちらも2つのベクトルの中間を計算するためのメソッドよ。Lerpは線形補間、Slerpは球面線形補間という違いがあるの。
Unityでは与えられた２つのベクトルを補間するメソッドとして、Vector3.Lerp()とVector3.Slerp()が用意されています。
両者とも、与えられた２つのベクトルを補間計算したベクトルを返すメソッドです。
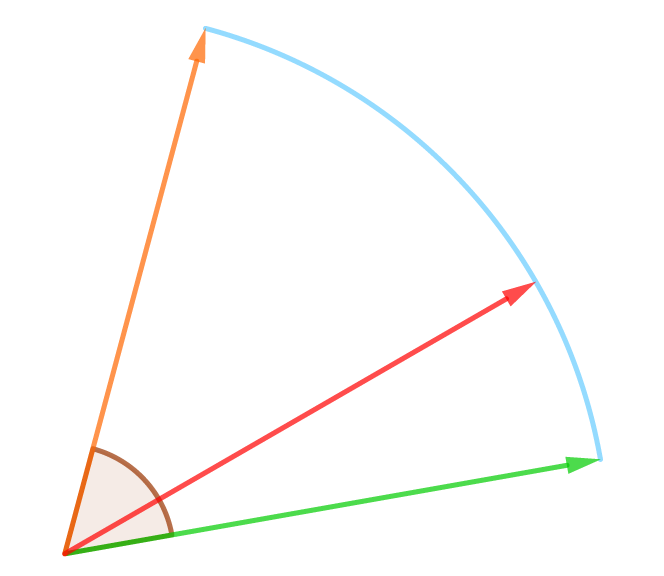
両者の結果のベクトルを可視化すると次のようになります。
緑色ベクトルはVector3.Lerp()、黄色ベクトルはVector3.Slerp()が返すベクトルです。Lerpのほうは一直線上で補間されるのに対し、Slerpは円弧を描くように補間されています。
本記事では、Vector3.Lerp()およびVector3.Slerp()メソッドの使い方について解説し、内部で行われている補間の計算処理についても触れておきます。
- Unity2021.1.16f1
Vector3.Lerp()メソッド
与えられた２つのベクトルを線形補間したベクトルを返すメソッドです。補間されたベクトルは、２つのベクトルの間を等速直線運動するような動きになります。
メソッドの形式は以下の通りです。
public static Vector3 Lerp(Vector3 a, Vector3 b, float t);引数a、bには補間対象となる２つのベクトルを指定します。
引数tには補間位置を 0～1の範囲で指定します。tが0のときはベクトルaと一致し、値が大きくなるほどベクトルbに近づいていき、1のときはbに一致します。
戻り値は、ベクトルa、bをtで線形補間したベクトルとなります。
Vector3.Slerp()メソッド
与えられた２つのベクトルを球面線形補間したベクトルを返すメソッドです。補間されたベクトルは、２つのベクトルを結ぶ球面に沿って等速移動するような動きをします。
２つのベクトルの長さが異なる場合、補間されるベクトルの長さは線形補間されます。
メソッドの形式は以下の通りです。
public static Vector3 Slerp(Vector3 a, Vector3 b, float t);引数の意味や戻り値はVector3.Lerp()と一緒です。
引数a、bに補間対象のベクトル、tに0～1の範囲で補間位置を指定します。
戻り値は、ベクトルa、bをtで球面線形補間したベクトルです。ベクトルの長さはベクトルa、bをtで線形補間した値となります。
使用例
実際にVector3.Lerp()、Vector3.Slerp()を使った例を紹介します。
Vector3.Lerp()による直線移動
２点間を等速で往復移動するサンプルスクリプトです。
using UnityEngine;
public class LerpPingPong : MonoBehaviour
{
// 線形補間の始点
[SerializeField] private Transform _from;
// 線形補間の終点
[SerializeField] private Transform _to;
// 移動時間[s]
[SerializeField] private float _duration = 1;
private void Update()
{
// 始点・終点の位置取得
var a = _from.position;
var b = _to.position;
// 補間位置計算
var t = Mathf.PingPong(Time.time / _duration, 1);
// 補間位置を反映
transform.position = Vector3.Lerp(a, b, t);
}
}移動させたいオブジェクトにアタッチし、インスペクターから各種パラメータを設定します。２点_from、_toはゲームオブジェクトで指定します。_durationには２点間を移動する時間を秒指定します。
実行結果
Vector3.Slerp()による円運動
２点を結ぶ円弧に沿って往復するサンプルスクリプトです。
using System;
using UnityEngine;
public class SlerpPingPong : MonoBehaviour
{
// 球面線形補間の始点
[SerializeField] private Transform _from;
// 球面線形補間の終点
[SerializeField] private Transform _to;
// 移動時間[s]
[SerializeField] private float _duration = 1;
// 円運動の中心点
[SerializeField] private Transform _sphereCenter;
private void Update()
{
// 始点・終点の位置取得
var a = _from.position;
var b = _to.position;
// 補間位置計算
var t = Mathf.PingPong(Time.time / _duration, 1);
// 円運動の中心点取得
var center = _sphereCenter.position;
// 円運動させる前に中心点が原点に来るように始点・終点を移動
a -= center;
b -= center;
// 原点中心で円運動
var slerpPos = Vector3.Slerp(a, b, t);
// 中心点だけずらした位置を戻す
slerpPos += center;
// 補間位置を反映
transform.position = slerpPos;
}
}１つ目のサンプルスクリプト同様、移動させたいオブジェクトにアタッチし、各種パラメータを設定します。
_centerには円運動の中心点となるオブジェクトを指定します。
実行結果
オレンジ色のブロックが円運動の中心で、その周りをSlerpによって球面線形補間された黄色ブロックが円弧を描くように移動していることが分かります。
補間の計算処理
ここまでLerpで線形補間、Slerpで球面線形補間する方法を解説しました。両者が内部的に行っている補間計算処理についても触れておきます。
線形補間
線形補間は次式で計算します。
\vec{p_l} = (1 - t) \vec{a} + t \vec{b}線形補間されたベクトル\vec{p_l}は、ベクトル\vec{a}、\vec{b}を1-t:tで内分した結果となります。
球面線形補間
Vector3.Slerp()が内部で行う球面線形補間は、ベクトルの長さと向きを線形補間するような挙動になっています。
計算式は次式のようになります。
\vec{p_s} = s \left\{ \frac{\sin{(1 - t) \theta}}{\sin{\theta}} \vec{e_a} + \frac{\sin{t \theta}}{\sin{\theta}} \vec{e_b} \right\}s = (1 - t) |\vec{a}| + t |\vec{b}|\vec{e_a} = \frac{\vec{a}}{|\vec{a}|}, \vec{e_b} = \frac{\vec{b}}{|\vec{b}|}ただし、|\vec{a}| \neq 0, |\vec{b}| \neq 0 , 0^{\circ} < \theta < 180^{\circ}
sはベクトルの長さに相当し、式の形は線形補間と一緒です。
\thetaはベクトル\vec{a}と\vec{b}とのなす角です。なす角\thetaは次式のように計算することが可能です。
\theta = \arccos{\frac{\vec{a} \cdot \vec{b}}{|\vec{a}| |\vec{b}|}}上式が成り立つ理由を知りたい方は、以下記事をご覧ください。
\vec{e_a}、\vec{e_b}はそれぞれ\vec{a}、\vec{b}を長さ１に正規化したベクトルです。球面線形補間するときは、元のベクトルの長さを揃える必要があるため正規化しています。中括弧内の式で半径１の球面上に沿った補間が行われます。
球面線形補間の式の証明
まず、\vec{a}、\vec{b}を正規化したベクトル\vec{e_a}、\vec{e_b}の球面線形補間に着目します。
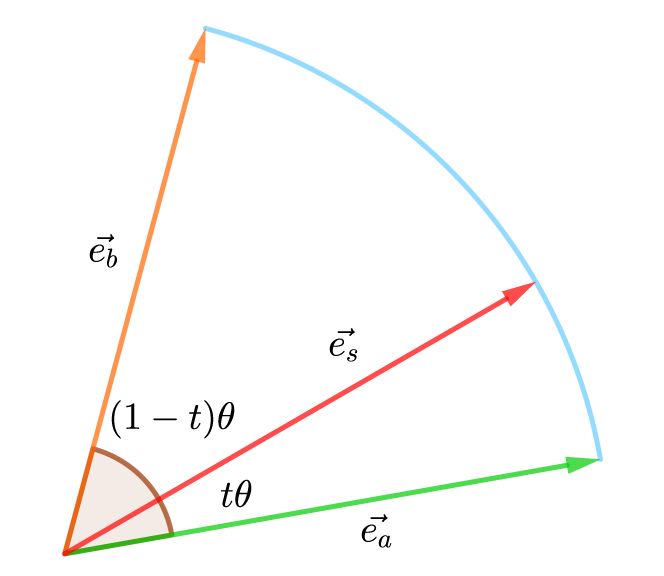
\vec{e_a}、\vec{e_b}をtで球面線形補間したベクトル\vec{e_s}は、次式のように表すことができます。
\vec{e_s} = s_a \vec{e_a} + s_b \vec{e_b}これを図示すると次のようになります。
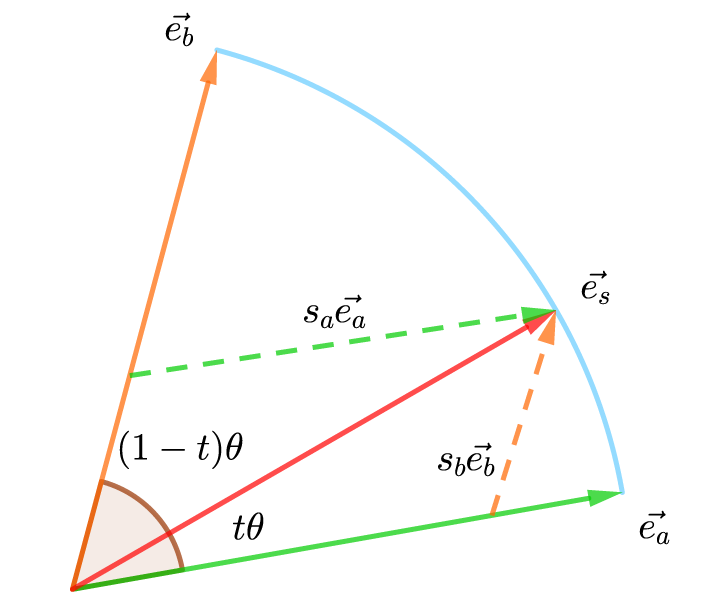
次の三角形に着目します。
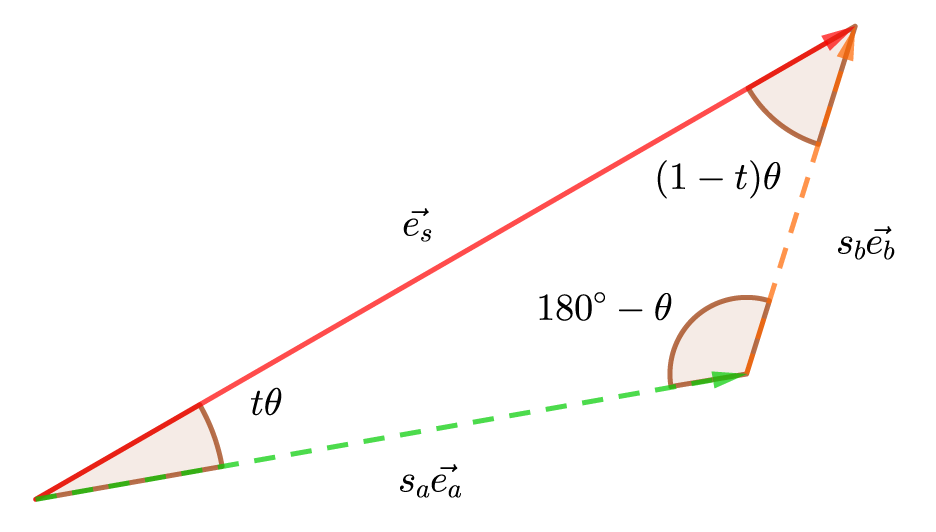
ベクトル\vec{e_s}、s_a \vec{e_a}、s_b \vec{e_b}の長さはそれぞれ1、s_a、s_bとなり、角度も定まります。
ここで、正弦定理を用いて次式のように表すことができます。
\frac{s_a}{\sin{(1-t)\theta}} = \frac{s_b}{\sin{t\theta}} = \frac{1}{\sin{(180^{\circ}-\theta)}} \tag{1}\sin{(180^{\circ}-\theta)} = \sin{\theta}となる性質を利用して、式(1)よりs_a、s_bが求まります。
s_a = \frac{\sin{(1-t)\theta}}{\sin{\theta}}s_b = \frac{\sin{t\theta}}{\sin{\theta}}したがって、\vec{e_s}は次式のようになります。
\vec{e_s} = \frac{\sin{(1-t)\theta}}{\sin{\theta}} \vec{e_a} + \frac{\sin{t\theta}}{\sin{\theta}} \vec{e_b} \tag{2}最終的に求めたいVector3.Slerp()の結果\vec{p_s}の長さsは\vec{a}と\vec{b}の長さをtで線形補間した値なので、次式のようになります。
s = (1-t) |\vec{a}| + t |\vec{b}|また、\vec{e_s}の長さが1であることから、\vec{p_s}は
\vec{p_s} = s \vec{e_s} \tag{3}と表すことができます。
式(2)を(3)に代入すると、\vec{p_s}が求まります。
\begin{aligned}
\vec{p_s} &= s \vec{e_s} \\
&= s \left\{ \frac{\sin{(1-t)\theta}}{\sin{\theta}} \vec{e_a} + \frac{\sin{t\theta}}{\sin{\theta}} \vec{e_b} \right\} \\
\end{aligned}計算式の確認
前述の球面線形補間の計算式が正しいかどうかを確認するスクリプトです。
using UnityEngine;
public class SlerpCompCheck : MonoBehaviour
{
[SerializeField] private Vector3 _from;
[SerializeField] private Vector3 _to;
[SerializeField, Range(0, 1)] private float _t;
private void Update()
{
// Vector3.Slerpによる計算
var slerp = Vector3.Slerp(_from, _to, _t);
// 自前計算
var mySlerp = MySlerp(_from, _to, _t);
// 計算結果の比較を出力
print($"Slerp = {slerp}, MySlerp = {mySlerp}, IsEqual = {slerp == mySlerp}");
}
// 自前の球面線形補間処理
private static Vector3 MySlerp(Vector3 a, Vector3 b, float t)
{
var na = a.normalized;
var nb = b.normalized;
var theta = Mathf.Acos(Vector3.Dot(na, nb));
var sinTheta = Mathf.Sin(theta);
var sinThetaFrom = Mathf.Sin((1 - t) * theta);
var sinThetaTo = Mathf.Sin(t * theta);
var magnitudeLerp = Mathf.Lerp(a.magnitude, b.magnitude, t);
var slerpVector = (sinThetaFrom * na + sinThetaTo * nb) / sinTheta;
return magnitudeLerp * slerpVector;
}
}球面線形補間の計算式を疑似的に実装し、結果が一致しているかを確認します。あくまでも計算式を検証するためのスクリプトなので、パフォーマンスは敢えて考慮していません。
実行結果
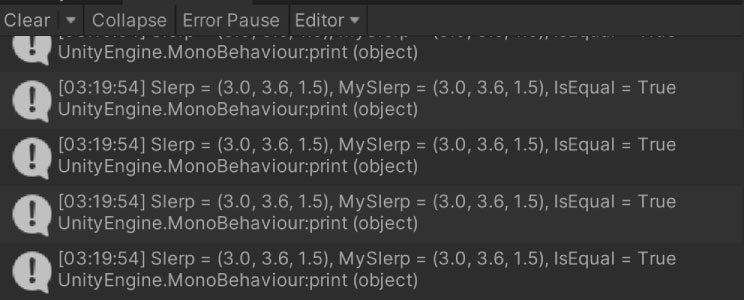
結果が一致していることを確認できました。
さいごに
Vector3.Lerp()による線形補間とVector3.Slerp()による球面線形補間の使い方と挙動について解説しました。
線形補間は２点間の移動、球面線形補間はある点を中心に回るような移動を実装するのに向いています。
Vector3.Slerp()が行う球面線形補間は、任意の２つのベクトルを指定できることから、長さは線形補間、向きは球面線形補間という２種類の計算しているのが特徴です。このことは公式リファレンスにも記載されていますが、計算式を立てて動作検証することができました。
ご参考にしていただければ幸いです。
