【Unity】重み付きの確率抽選を行う方法

2022年9月24日

こじゃらこじゃら

異なる確率でアイテムをドロップさせたりゲットさせたりする方法を教えて欲しいの。

このはこのは

重み付き抽選のアルゴリズムを実装すれば可能だわ。

異なる出現確率の要素をランダムに抽選する方法の解説記事です。

次のように、要素ごとに重みが付けられ、全体に対する重みの割合が高いほど高確率で出現させたりするケースを想定します。

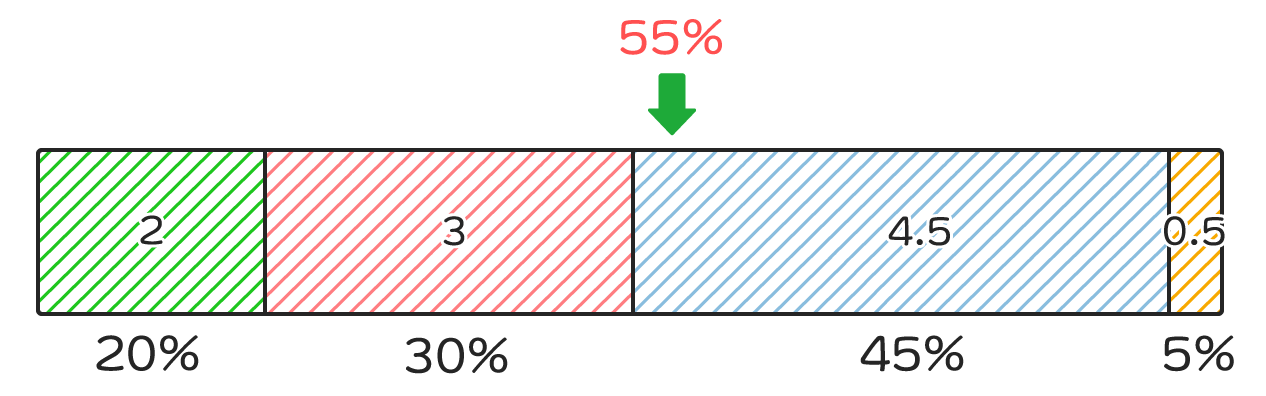
このような重み付き抽選を行うには、抽選する度にループを回す必要があります。しかしながら、特定のケースにおいてはメモリを消費する代わりに抽選処理を高速化できます。

本記事では、ループを活用した標準的な抽選アルゴリズムの実装方法を解説し、高速化する方法についても触れます。また、高速化前と後でどれくらいパフォーマンスに差が出るかの検証結果も示します。

動作環境
  • Unity 2022.1.16f1

スポンサーリンク

目次 非表示

想定する状況

Unityのスクリプト側で重み付き抽選のロジックを実装して使用することを想定します。

本記事では、アルゴリズムの本質的な部分に絞った解説をするため、クラス設計等については敢えて触れません。

注意

オンラインゲームにおけるガチャなどデータの改ざんが懸念される場面においては、サーバー上でロジックを実装することを推奨します。本記事で解説するアルゴリズム部分は、Unity以外の環境でも適用可能です。

ループを用いて重み付き抽選を行う

最初に、ループを用いて抽選を行うアルゴリズムについて紹介します。

要素数に比例して計算量が増大する傾向がありますが、メモリの消費が少ない 、実装が簡単というメリットがあります。

この方法は、以下リファレンスのページでも紹介されています。

参考：ランダムなゲームプレイ要素の追加 – Unity マニュアル

アルゴリズム

まず、重み全体の総和を計算し、0～総和までの範囲の乱数値を取得します。

次に、要素の先頭から順に、乱数値と現在要素までの重みの総和の大小関係を調べ、乱数値が総和より下回るまで繰り返します。

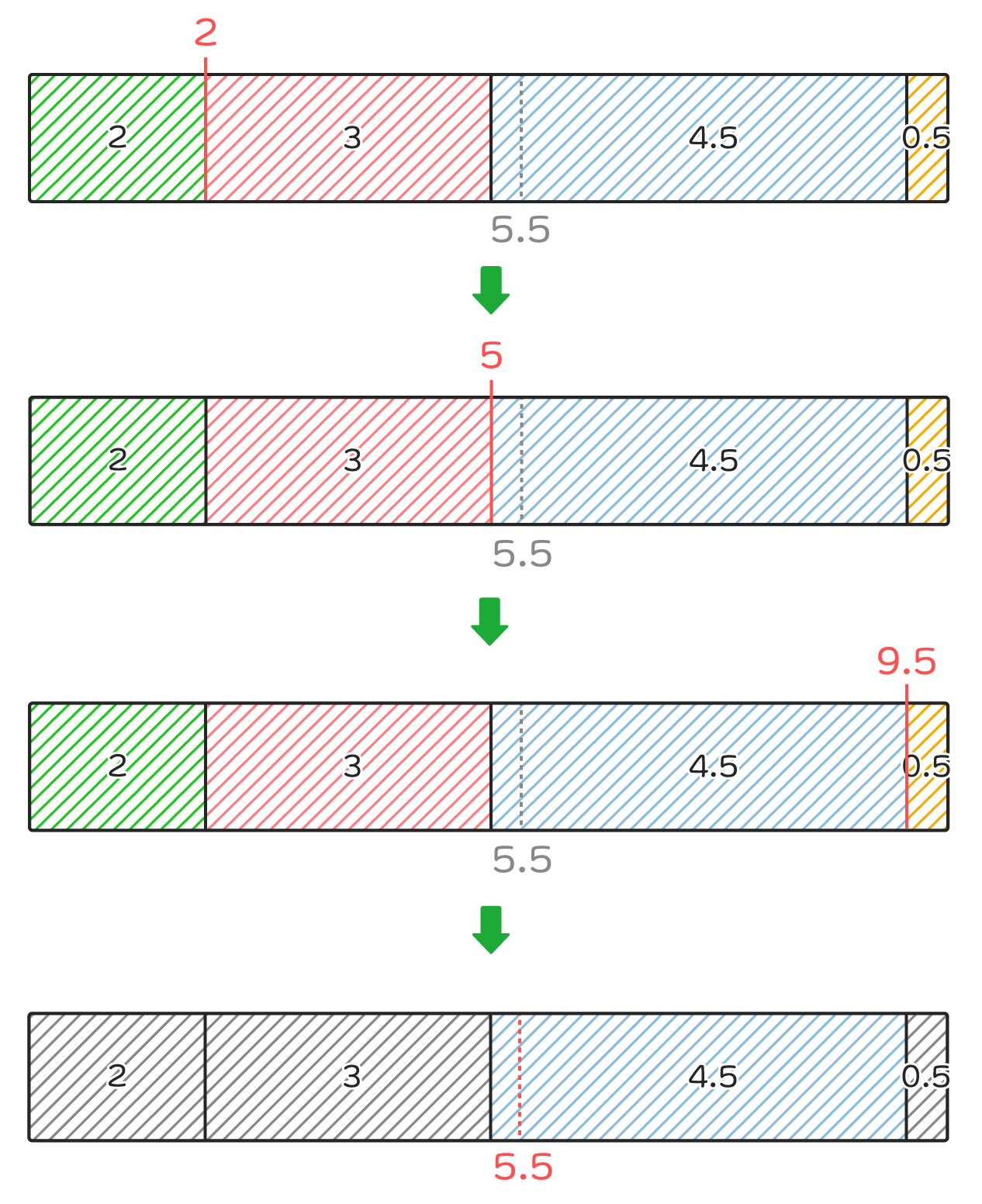
繰り返しが終了したときの現在要素が最終的な抽選結果となります。

このように要素の先頭から順番に大小関係をチェックしていくため、１回の抽選処理にかかる最大時間は要素数に比例します。（時間計算量O(n)）

サンプルスクリプト

ここまでのアルゴリズムを実装した例です。

スペースキーを押している間、重み付き抽選を行い結果を出力し続けます。

WeightedChooser.cs
/// <summary>
/// 重み付き確率抽選クラス
/// </summary>
public class WeightedChooser
{
    // 各要素の重みリスト
    private float[] _weights;
    
    // 重みの総和（初期化時に計算される）
    private float _totalWeight;

    /// <summary>
    /// コンストラクタ
    /// </summary>
    /// <param name="weights">重みリスト</param>
    public WeightedChooser(float[] weights)
    {
        _weights = weights;
        
        // 重みの総和計算
        for (var i = 0; i < _weights.Length; i++)
        {
            _totalWeight += _weights[i];
        }
    }
    
    /// <summary>
    /// 重み付きの確率抽選を実施する
    /// </summary>
    /// <returns>選択された要素のインデックス</returns>
    public int Choose()
    {
        // 0～重みの総和の範囲の乱数値取得
        var randomPoint = UnityEngine.Random.Range(0, _totalWeight);

        // 乱数値が属する要素を先頭から順に選択
        var currentWeight = 0f;
        for (var i = 0; i < _weights.Length; i++)
        {
            // 現在要素までの重みの総和を求める
            currentWeight += _weights[i];

            // 乱数値が現在要素の範囲内かチェック
            if (randomPoint < currentWeight)
            {
                return i;
            }
        }

        // 乱数値が重みの総和以上なら末尾要素とする
        return _weights.Length - 1;
    }
}
LogViewer.cs
using UnityEngine;

public class LogViewer : MonoBehaviour
{
    // 各要素の重みリスト
    [SerializeField] private float[] _weights;

    private WeightedChooser _weightedChooser;
    
    // 内部データ初期化
    private void Awake()
    {
        _weightedChooser = new WeightedChooser(_weights);
    }

    #region Test

    private void Update()
    {
        // スペースキーを押している間、選択要素を出力し続ける
        if (Input.GetKey(KeyCode.Space))
        {
            var index = _weightedChooser.Choose();
            Debug.Log($"抽選された要素 : {index}");
        }
    }

    #endregion
}

上記スクリプトをそれぞれWeightedChooser.cs、LogViewer.csという名前で保存し、Weighted Chooserコンポーネントを適当なゲームオブジェクトにアタッチし、インスペクターよりWeights項目を設定すると機能するようになります。

上記はあくまでも例のため、実際の開発で利用する場合は、場面に適したクラス設計をすることをお勧めします。

実行結果

次のようにスペースキーを押している間、選択された要素のインデックスがログ出力されます。

概ね設定した重み通りの割合で要素が抽選されていることが確認できました。

スクリプトの説明

以下コードで各要素の全体の重みの総和を事前に求めています。

// 重みの総和計算
for (var i = 0; i < _weights.Length; i++)
{
    _totalWeight += _weights[i];
}

そして、抽選処理の最初の部分で乱数値を取得しています。

// 0～重みの総和の範囲の乱数値取得
var randomPoint = UnityEngine.Random.Range(0, _totalWeight);

得られた乱数値がどの要素に属しているかを以下ループでチェックしています。

// 乱数値が属する要素を先頭から順に選択
var currentWeight = 0f;
for (var i = 0; i < _weights.Length; i++)
{
    // 現在要素までの重みの総和を求める
    currentWeight += _weights[i];

    // 乱数値が現在要素の範囲内かチェック
    if (randomPoint < currentWeight)
    {
        return i;
    }
}

// 乱数値が重みの総和以上なら末尾要素とする
return _weights.Length - 1;

抽出処理を高速化する

前述の方法では、抽選処理を行う度に最大で要素数に比例した計算量が掛かっていました。これは、乱数値がどの要素に属するかを先頭から順番にチェックしていたためです（線形探索）。

これは、二分探索のアルゴリズムを適用することで、要素に比例したメモリ消費を行う代わりに計算量を劇的に減らすことが可能です。

時間計算量空間計算量
高速化前（線形探索）O(n)O(1)
高速化後（二分探索）O(\log n)O(n)
抽選処理の処理負荷

ただし、初期化時や要素の重みの更新時に、要素数に比例した計算量がかかるという欠点があります。そのため、重みの値や要素があまり変わらない、かつ要素数が多いときに真価を発揮する方法とも言えます。

アルゴリズム

最初に、重みの総和と共に各要素までの重みの総和の情報（配列）を事前計算で作成しておきます。

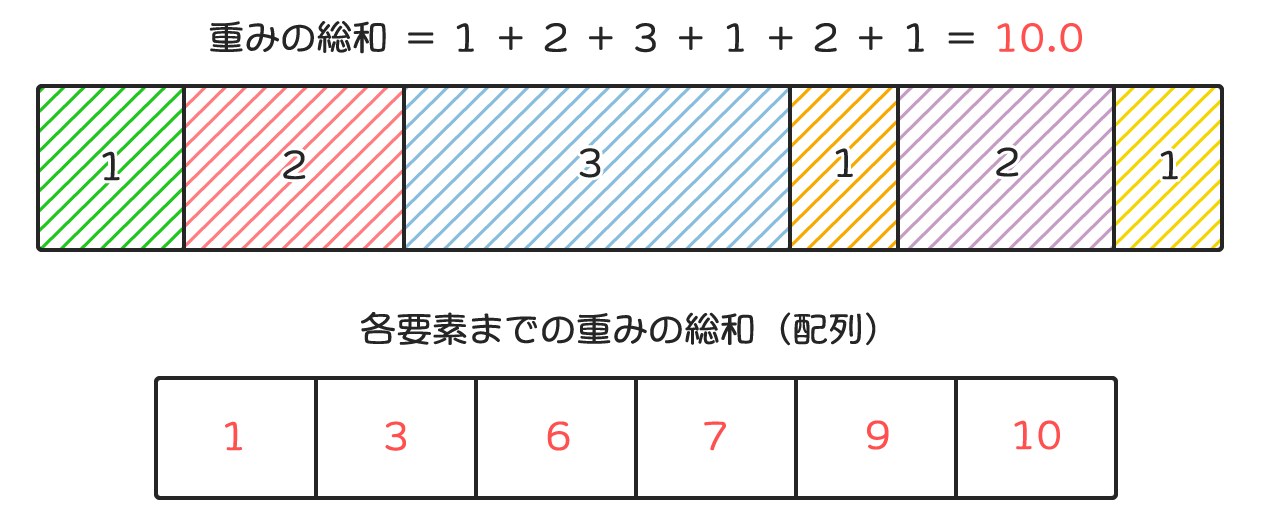
そして、抽選処理を実行するときに、０～重みの総和の範囲の乱数値を取得します。

乱数値がどの要素に属するかの判定は、１つ目の例と同様の手順で判定可能ですが、各要素までの重みの総和配列は昇順にソートされているので二分探索によるチェックが可能です。

二分探索では、次のように探索範囲の中央要素と探索対象との大小を比較し、候補から外れた半分の領域を除外していくような流れで探索範囲を絞っていきます。

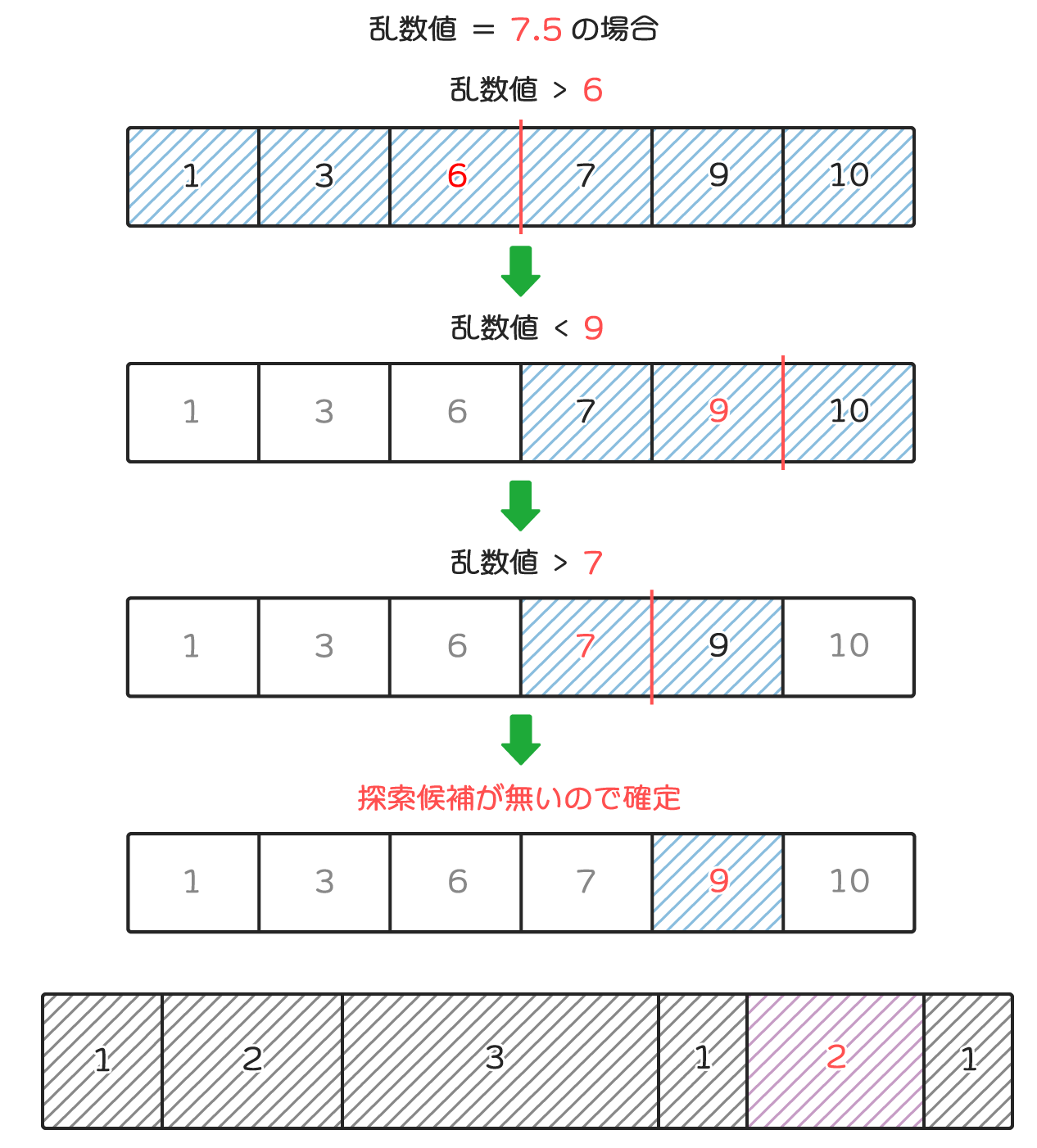
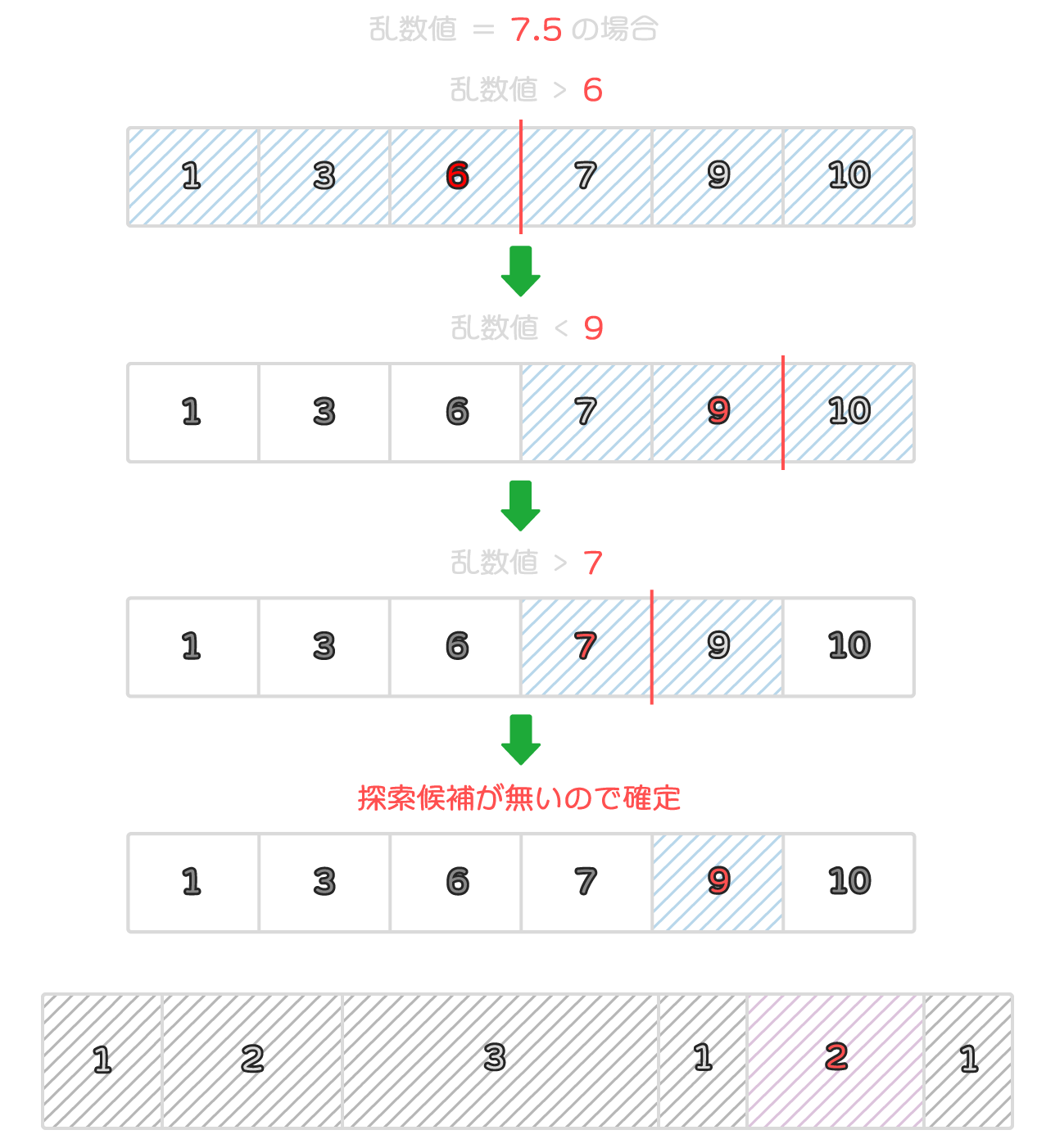
例では、乱数値7.5が7～9の範囲の要素に属するため、先頭から５番目の要素に決定されます。

抽出処理を高速化できるのは、探索のループを回す度に半分ずつ探索範囲が狭まっていくような挙動になるためです。

サンプルスクリプト

以上の高速化の流れを実装したサンプルスクリプトです。

WeightedChooserFast.cs
/// <summary>
/// 重み付き確率抽選クラス（高速化後）
/// </summary>
public class WeightedChooserFast
{
    // 各要素の重みリスト
    private float[] _weights;
    
    // 重みの総和（初期化時に計算される）
    private float _totalWeight;

    // 重みの累積テーブル
    private float[] _cumulativeWeights;

    /// <summary>
    /// コンストラクタ
    /// </summary>
    /// <param name="weights">重みリスト</param>
    public WeightedChooserFast(float[] weights)
    {
        _weights = weights;
        
        // 重みの総和計算・各要素までの重みの総和計算
        _cumulativeWeights = new float[_weights.Length];
        
        for (var i = 0; i < _weights.Length; i++)
        {
            _totalWeight += _weights[i];
            _cumulativeWeights[i] = _totalWeight;
        }
    }
    
    /// <summary>
    /// 重み付きの確率抽選を実施する
    /// </summary>
    /// <returns>選択された要素のインデックス</returns>
    public int Choose()
    {
        // 0～重みの総和の範囲の乱数値取得
        var randomPoint = UnityEngine.Random.Range(0, _totalWeight);

        // 乱数値が属する要素を二分探索
        var minIndex = 0;
        var maxIndex = _cumulativeWeights.Length - 1;

        while (minIndex < maxIndex)
        {
            // 探索範囲の中央要素取得
            var centerIndex = (minIndex + maxIndex) / 2;
            var centerPoint = _cumulativeWeights[centerIndex];

            // 乱数値は現在要素の範囲外かどうか
            if (randomPoint > centerPoint)
            {
                // 範囲外なら後半を探索範囲に絞る
                minIndex = centerIndex + 1;
            }
            else
            {
                // 現在要素の範囲の下限（前要素の上限）取得
                var prevPoint = centerIndex > 0 ? _cumulativeWeights[centerIndex - 1] : 0;

                // 乱数値が現在要素の下限と上限の間なら確定
                if (randomPoint >= prevPoint)
                {
                    return centerIndex;
                }

                // 前半を探索範囲に絞る
                maxIndex = centerIndex;
            }
        }

        // 探索範囲が１要素しかなくなったら確定
        return maxIndex;
    }
}
LogViewerFast .cs
using UnityEngine;

internal class LogViewerFast : MonoBehaviour
{
    // 各要素の重みリスト
    [SerializeField] private float[] _weights;

    private WeightedChooserFast _weightedChooser;
    
    // 内部データ初期化
    private void Awake()
    {
        _weightedChooser = new WeightedChooserFast(_weights);
    }

    #region Test

    private void Update()
    {
        // スペースキーを押している間、選択要素を出力し続ける
        if (Input.GetKey(KeyCode.Space))
        {
            var index = _weightedChooser.Choose();
            Debug.Log($"抽選された要素 : {index}");
        }
    }

    #endregion
}

上記をそれぞれWeightedChooserFast.cs、LogViewerFast .csという名前で保存し、Weighted Chooser Fastコンポーネントを適当なゲームオブジェクトにアタッチすると機能するようになります。

使用方法および実行結果は、１つ目の例と一緒のため割愛します。

スクリプトの説明

初期化処理では、重みの総和のほか、各要素までの重みの累積を計算しています。

// 重みの総和計算・各要素までの重みの総和計算
_cumulativeWeights = new float[_weights.Length];

for (var i = 0; i < _weights.Length; i++)
{
    _totalWeight += _weights[i];
    _cumulativeWeights[i] = _totalWeight;
}

重み付き抽選を行うChooseメソッドでは二分探索を用いて要素を検索するため、次のように探索範囲の下限と上限を定めます。

// 乱数値が属する要素を二分探索
var minIndex = 0;
var maxIndex = _cumulativeWeights.Length - 1;

そして、以下のwhileループで二分探索を実施し、対象を絞り込みながら乱数値が重みの範囲内にあるかどうかをチェックしています。

while (minIndex < maxIndex)
{
    // 探索範囲の中央要素取得
    var centerIndex = (minIndex + maxIndex) / 2;
    var centerPoint = _cumulativeWeights[centerIndex];

    // 乱数値は現在要素の範囲外かどうか
    if (randomPoint > centerPoint)
    {
        // 範囲外なら後半を探索範囲に絞る
        minIndex = centerIndex + 1;
    }
    else
    {
        // 現在要素の範囲の下限（前要素の上限）取得
        var prevPoint = centerIndex > 0 ? _cumulativeWeights[centerIndex - 1] : 0;

        // 乱数値が現在要素の下限と上限の間なら確定
        if (randomPoint >= prevPoint)
        {
            return centerIndex;
        }

        // 前半を探索範囲に絞る
        maxIndex = centerIndex;
    }
}

// 探索範囲が１要素しかなくなったら確定
return maxIndex;

乱数値が要素の重みの範囲内、または探索範囲が要素１つ分しかなくなったら確定とみなします。

２つのアルゴリズムの実行速度の比較

ここまで紹介した2つの例でどれくらいパフォーマンスに差が出ているかの検証結果を示します。

以下、計測用のスクリプトです。

RandomChooserPerformanceTests.cs
using System.Text;
using UnityEngine;

public class RandomChooserPerformanceTests : MonoBehaviour
{
    private void Update()
    {
        // スペースキーが押されたら計測開始
        if (Input.GetKeyDown(KeyCode.Space))
        {
            RunTests("ケース1", 100, 10000);
            RunTests("ケース2", 10000, 10000);
            RunTests("ケース3", 1000000, 10000);
        }
    }

    private void RunTests(string title, int elementCount, int iterationCount)
    {
        // テストデータ作成
        var weights = new float[elementCount];
        for (var i = 0; i < weights.Length; i++)
        {
            weights[i] = UnityEngine.Random.Range(0f, 100f);
        }

        var chooser1 = new WeightedChooser(weights);
        var chooser2 = new WeightedChooserFast(weights);

        var stopWatch = new System.Diagnostics.Stopwatch();

        // 高速化前の処理時間計測
        stopWatch.Start();
        for (var i = 0; i < iterationCount; i++)
        {
            chooser1.Choose();
        }

        stopWatch.Stop();
        var elapsedTime1 = stopWatch.Elapsed;

        stopWatch.Reset();

        // 高速化後の処理時間計測
        stopWatch.Start();
        for (var i = 0; i < iterationCount; i++)
        {
            chooser2.Choose();
        }

        stopWatch.Stop();
        var elapsedTime2 = stopWatch.Elapsed;

        // 計測結果をログ出力
        var result = new StringBuilder();
        result.AppendLine($"===== {title} =====");
        result.AppendLine($"要素数 : {elementCount}, 実行回数 : {iterationCount}");
        result.AppendLine($"実行時間（高速化前） : {elapsedTime1}");
        result.AppendLine($"実行時間（高速化後） : {elapsedTime2}");

        Debug.Log(result.ToString());
    }
}

上記スクリプトをRandomChooserPerformanceTests.csという名前で保存し、適当なゲームオブジェクトにアタッチすると機能します。

スペースキーを押す度に時間計測が開始され、終了するとコンソールログに結果が出力されます。

時間計測には、System.Diagnostics.Stopwatchクラスを使用しました。

実行結果

高速化前と高速化後の実行時間は以下のようになりました。

要素数実行回数高速化前の実行時間（秒）高速化後の実行時間（秒）
100100000.0027s0.00089s
10000100000.22s0.0015s
10000001000022.0s0.003s

高速化前では要素数に比例して時間が増えているのに対し、高速化後では要素数が増えてもそれほど大きく増えていないことが分かります。

このことから、要素数が大きくなるほど高速化アルゴリズムの恩恵を受けると言って良いでしょう。要素数が極端に少ない場合は、どちらでもそれほど大きく差が出ないと言えます。

また、高速化後では、頻繁に重みが更新されるケースにおいては差異が出ないか、逆に遅くなってしまう可能性もあり得るため注意が必要です。

さいごに

重み付きの確率抽選を行う2種類の方法について解説しました。

要素数と要素の更新頻度、抽選の実行回数などによってどちらの方法が適しているか変わってくる可能性があります。

それぞれの特徴を押さえた上で使い分けると良いでしょう。

参考サイト

スポンサーリンク

前の記事

【Unity】Input Fieldでモバイル向けキーボードを…

次の記事

【Unity】Input Systemでピンチやマルチスワイプ…