【Unity2022】Splinesパッケージの内部計算式

UnityのSplinesパッケージの曲線はどのように計算されているの？

ベジェ曲線の補間計算式が用いられているわ。具体的に説明していくね。

Unity公式のスプライン（Splinesパッケージ）内部で行われているスプライン補間の計算処理についての解説記事です。

スプライン補間は、次のような動きを実現するために使われます。

スプライン補間の例

スプラインに沿って移動する（SplineAnimate）
スプラインをメッシュとして生成する（SplineExtrude）

Splinesパッケージでは、このような補間処理に3次ベジェ曲線の補間計算式が使用されています。

また、制御点間で補間される位置は、近似的に一定の速さで移動するような補正がかけられています。

複数の制御点を通るスプラインは、複数のベジェ曲線を繋げた曲線として表現されます。プログラムでは３次ベジェ曲線情報のリストとして保持されます。

本記事では、Splinesパッケージの内部で行われている補間計算式や速さの補正処理などの内部処理について解説していきます。

動作環境

Unity 2022.1.23f1
Splines 1.0.1

目次非表示

前提条件

Unity 2022.1以降でUnityプロジェクトが開かれており、Splinesパッケージがインストールされているものとします。

Splinesパッケージのインストール方法および使い方については、以下記事で解説しておりますので、必要な方はご覧ください。

【Unity2022】スプラインツールの導入方法と使い方

Unity 2022.1 TECH ストリームがリリースされてから、Unity公式のスプラインツールが使えるようになりました。 Unity 2022.1以降では、次のようなことがサードパーティー製アセットなしで実現できま…

2022年5月16日

ベジェ曲線の補間計算式

Splinesパッケージで使用される３次ベジェ曲線は、下図のように４つの制御点を元に決定される曲線として表現されます。

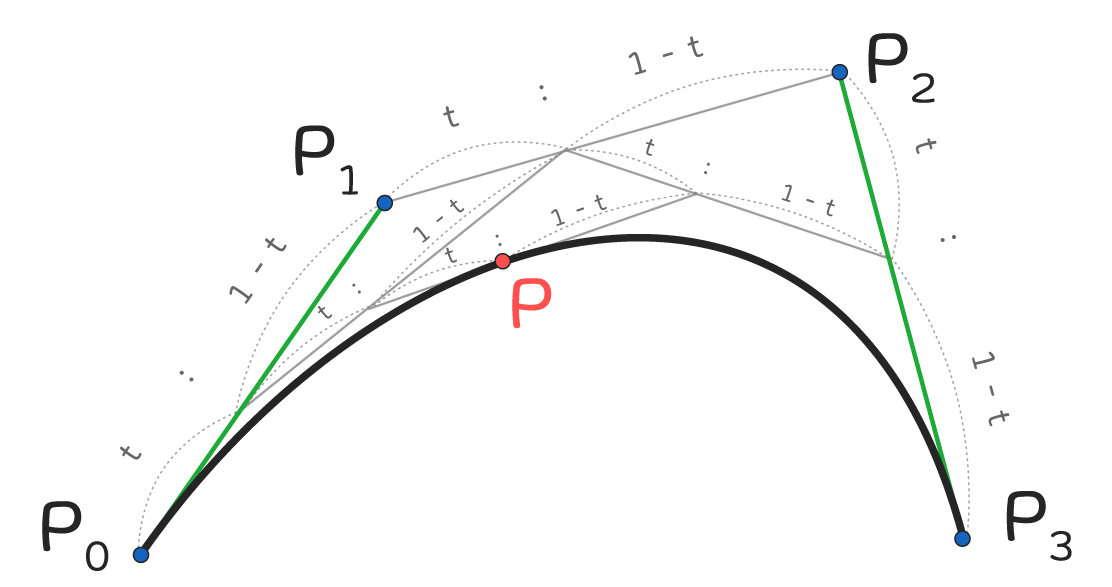
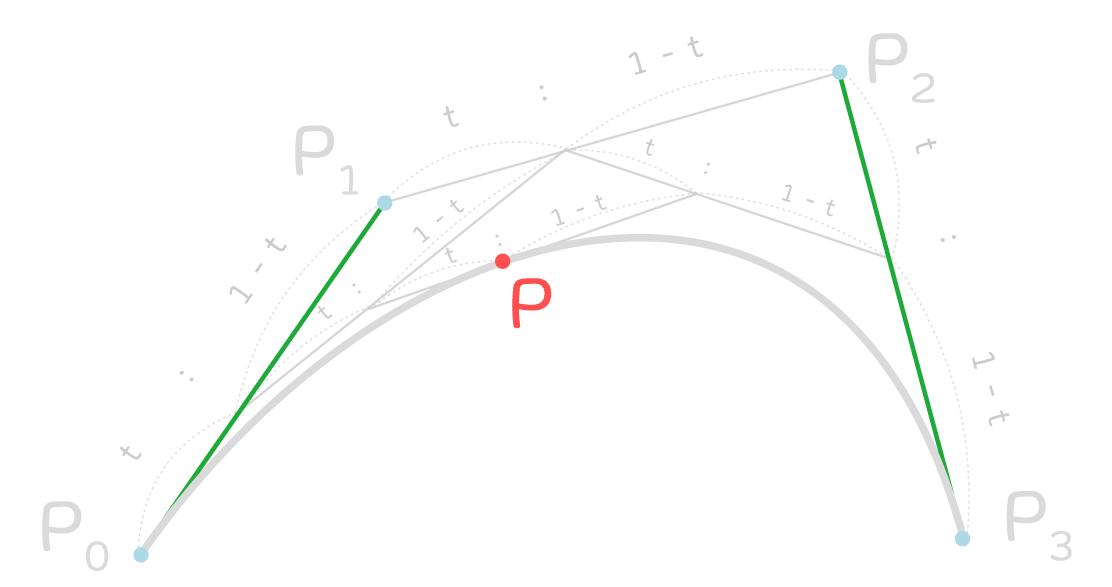
上図の補間された点 $P$ は、点 $P_0$ と点 $P_3$ を結ぶ曲線上の位置です。

$t$ が0から1に変化するとき、点 $P$ は $P_0$ から $P_３$ まで曲線に沿って移動するような挙動をします。

点 $P$ の位置は、４つの制御点 $P_0$ 、 $P_1$ 、 $P_2$ 、 $P_3$ と割合 $t$ を用いて、次の補間計算式で表されます。^[1]

３次ベジェ曲線の式

P = (1-t)^3 P_0 + 3t (1-t)^2 P_1 + 3t^2 (1-t) P_2 + t^3 P_3

ただし、 $0 \leq t \leq 1$

上式は、n次ベジェ曲線の一般系の式を $n=4$ として整理したものです。^[2]

ベジェ曲線の一般系は、n個の制御点 $P_0, P_1, \cdots , P_{n-1}$ からなる次式として表現されます。

ベジェ曲線の一般系

P = \sum_{i=0}^{n-1} {}_{n-1} \mathrm{C}_i t^i (1-t)^{n-i-1} P_i

{}_{n-1} \mathrm{C}_i = \dfrac{(n-1)!}{i! (n-i-1)!}

ただし、 $0 \leq t \leq 1$

参考：ベジエ/スプライン曲線

補間計算式のヘルパーAPI

前述の３次ベジェ曲線の補間計算式は、CurveUtility.EvaluatePositionメソッドから計算できます。

public static float3 EvaluatePosition(BezierCurve curve, float t)

参考：Class CurveUtility | Splines | 1.0.1

第１引数には、３次ベジェ曲線を指定します。これは、４つの制御点 $P_0$ 、 $P_1$ 、 $P_2$ 、 $P_3$ で表現されるベジェ曲線の構造体です。各制御点は３次元座標のfloat3型です。

参考：Struct BezierCurve | Splines | 1.0.1

第２引数には、0～1の範囲の割合 $t$ を指定します。

戻り値は、 $t$ で補間されたベジェ曲線上の３次元位置です。

サンプルスクリプト

CurveUtility.EvaluatePositionメソッドを用いて補間位置を求めるスクリプトです。

EvaluatePositionExample.cs

using UnityEngine;
using UnityEngine.Splines;

public class EvaluatePositionExample : MonoBehaviour
{
    // 各制御点オブジェクト
    [SerializeField] private Transform _p0Object, _p1Object, _p2Object, _p3Object;

    // 割合
    [SerializeField, Range(0, 1)] private float _t;

    // 補間された位置
    [SerializeField] private Transform _resultObject;

    private void Update()
    {
        // 各制御点のワールド座標取得
        var p0 = _p0Object.position;
        var p1 = _p1Object.position;
        var p2 = _p2Object.position;
        var p3 = _p3Object.position;

        // ベジェ曲線上の位置を取得
        var p = CurveUtility.EvaluatePosition(new BezierCurve(p0, p1, p2, p3), _t);

        // 結果に反映
        _resultObject.position = p;
    }
}

上記をEvaluatePositionExample.csという名前でUnityプロジェクトに保存し、適当なゲームオブジェクトにアタッチし、インスペクターより各種項目を設定すると機能するようになります。

例では、次のように白い球を制御点、黄色いキューブを計算結果の位置として反映することとします。

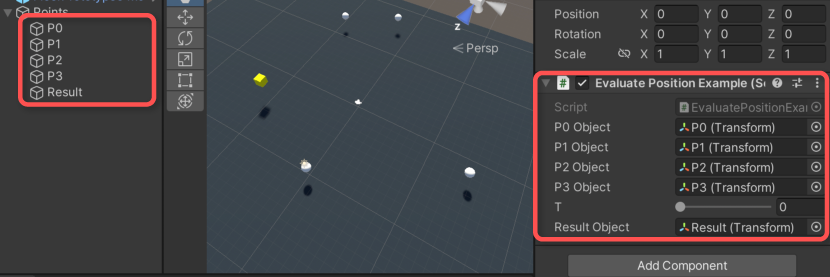
実行結果

インスペクターより $t$ の値を編集すると、ベジェ補間されるようになりました。

この時、割合 $t$ が一定の速さで変化しても、計算結果の位置は一定の速さで変化するわけではありません。

Splinesパッケージでは、上記の速さが一定になるような補正処理を、スプラインの長さに基づいて行っています。

ベジェ曲線の長さの計算

Splinesパッケージでは、スプラインの曲線の長さ（道のり）を近似的に計算することができます。

スプラインの長さは、次のように曲線をいくつかのセグメントに分割し、各点間の距離の総和として計算しています。

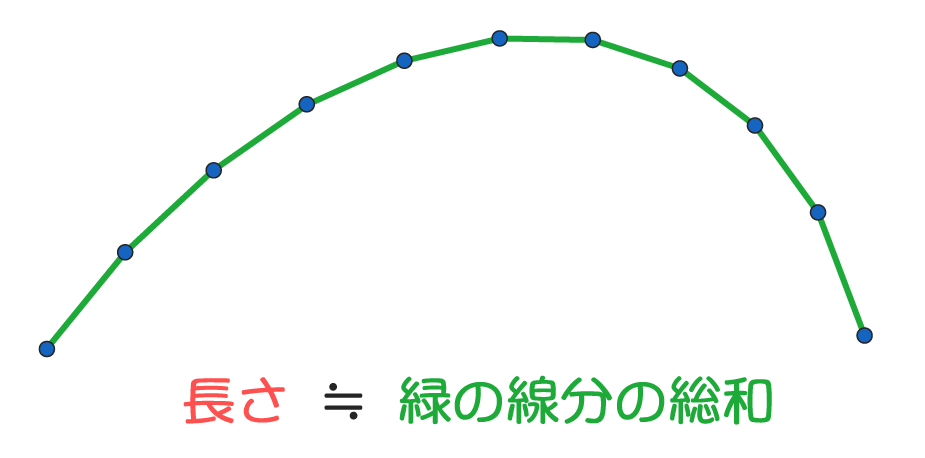
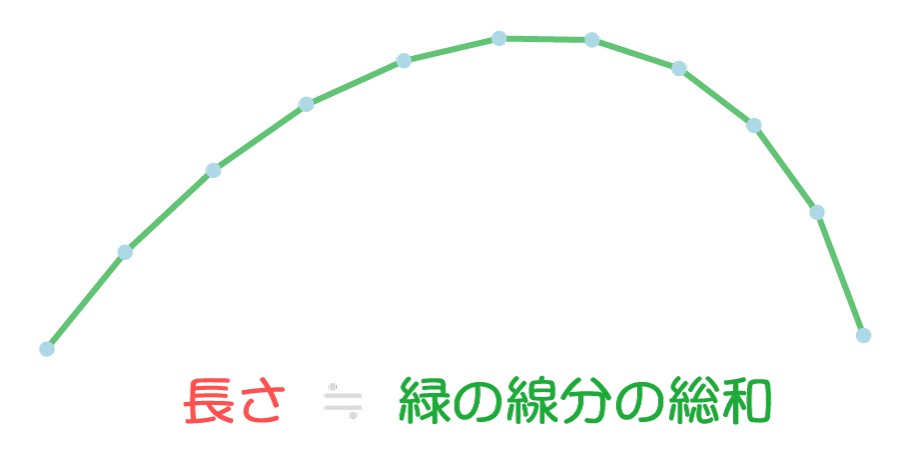
分割した各点位置を $P_0$ 側から順に $S_0, S_1, \cdots, S_n$ とすると、近似された長さは次式のようになります。

長さの近似式

L = \sum_{i=1}^n | S_i - S_{i-1} |

また、始点 $S_0$ から各セグメントの点 $S_i$ までの距離をルックアップテーブルとして取得することも可能です。このテーブルは、スプライン上を移動する速さを一定に保つ補正処理で内部的に使用されます。

近似した長さを求めるヘルパーAPI

CurveUtility.CalculateLengthメソッドで計算できます。

public static float CalculateLength(BezierCurve curve, int resolution = 30)

第１引数にはベジェ曲線の構造体を、第２引数には分割するセグメント数を指定します。

第２引数を省略すると、セグメント数が30として処理されます。

戻り値として、近似的な長さが返されます。

参考：Class CurveUtility | Splines | 1.0.1

サンプルスクリプト

ベジェ曲線の長さを指定されたセグメント数で計算する例です。

CalculateLengthExample.cs

using UnityEngine;
using UnityEngine.Splines;

public class CalculateLengthExample : MonoBehaviour
{
    // 各制御点オブジェクト
    [SerializeField] private Transform _p0Object, _p1Object, _p2Object, _p3Object;

    // セグメントの分割数
    [SerializeField] private int _resolution = 30;

    private void Update()
    {
        // 各制御点のワールド座標取得
        var p0 = _p0Object.position;
        var p1 = _p1Object.position;
        var p2 = _p2Object.position;
        var p3 = _p3Object.position;

        // ベジェ曲線の長さを計算
        var length = CurveUtility.CalculateLength(
            new BezierCurve(p0, p1, p2, p3),
            _resolution
        );
        
        // 結果をログ出力
        Debug.Log($"Length = {length}");
    }
}

上記スクリプトをCalculateLengthExample.csという名前で保存し、同様に適当なゲームオブジェクトにアタッチし、各制御点のオブジェクトを指定すると機能するようになります。

実行結果

セグメント数を大きくするほど精度が上がり、本来の曲線の長さに近づいていきます。

ただし、計算量もセグメント数に比例して増大していきます。

距離のルックアップテーブルを取得する

前述の曲線の長さは、ルックアップテーブルとして始点から各セグメントの点までの距離と割合の情報を配列として取得することもできます。

取得にはCurveUtility.CalculateCurveLengthsメソッドを使用します。

public static void CalculateCurveLengths(BezierCurve curve, DistanceToInterpolation[] lookupTable)

第１引数には、ベジェ曲線の構造体を指定します。

第２引数には、各セグメントの点までの距離を受け取るためのルックアップテーブル（配列）を指定します。

この配列は引数に渡す前に予め確保しておく必要があります。配列の要素数がそのまま分割するセグメント数になります。

参考：Class CurveUtility | Splines | 1.0.1

サンプルスクリプト

ベジェ曲線のルックアップテーブルを取得してログ出力するサンプルです。

CalculateCurveLengthsExample.cs

using System.Text;
using UnityEngine;
using UnityEngine.Splines;

public class CalculateCurveLengthsExample : MonoBehaviour
{
    // 各制御点オブジェクト
    [SerializeField] private Transform _p0Object, _p1Object, _p2Object, _p3Object;

    // セグメントの分割数
    [SerializeField] private int _resolution = 10;

    // 各セグメントの点までの長さと割合を格納するルックアップテーブル
    private DistanceToInterpolation[] _lookUpTable;
    
    private void Awake()
    {
        // ルックアップテーブルを予め作成
        _lookUpTable = new DistanceToInterpolation[_resolution];
    }

    private void Update()
    {
        // 各制御点のワールド座標取得
        var p0 = _p0Object.position;
        var p1 = _p1Object.position;
        var p2 = _p2Object.position;
        var p3 = _p3Object.position;

        // ルックアップテーブルを取得
        CurveUtility.CalculateCurveLengths(
            new BezierCurve(p0, p1, p2, p3),
            _lookUpTable
        );
        
        // 結果をログ出力
        var sb = new StringBuilder();
        
        for (var i = 0; i < _lookUpTable.Length; i++)
        {
            var row = _lookUpTable[i];
            sb.AppendLine($"[{i}] distance = {row.Distance}, t = {row.T}");
        }
        
        Debug.Log(sb);
    }
}

使い方は先の例とほぼ一緒です。適当なゲームオブジェクトにアタッチし、各種制御点となるオブジェクトを指定すると機能します。

実行結果

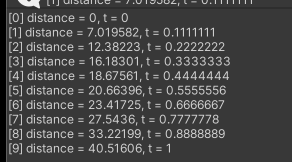
ベジェ曲線の各セグメントの点における距離と割合がログとして出力されます。

ベジェ曲線上の速さを一定にする

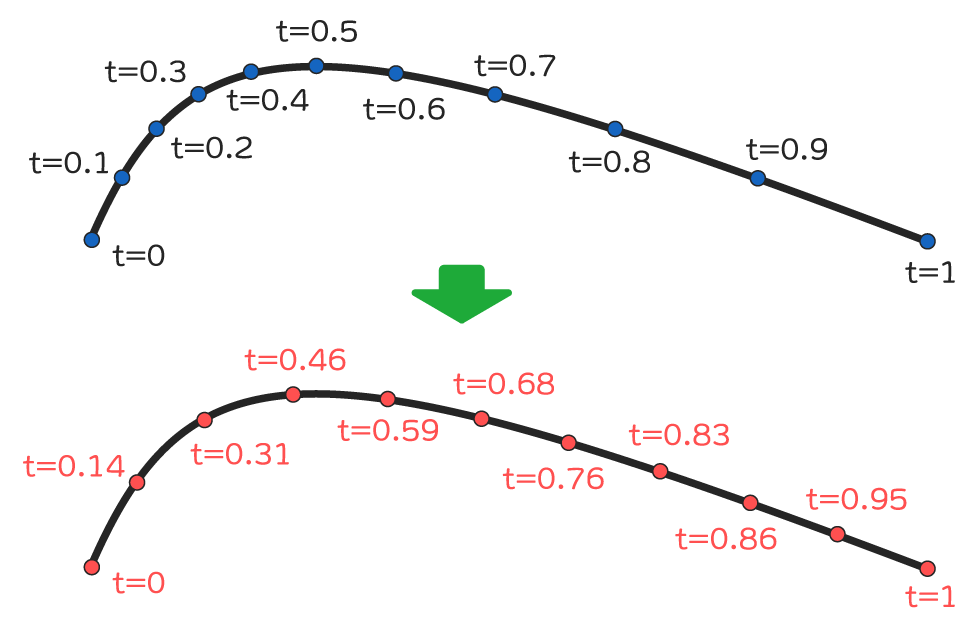
Splinesパッケージのスプライン補間では、割合 $t$ が一定の速さで変化するとき、補間した点も近似的に一定の速さで移動するような補正が行われます。

このような補正は、速さが一定になるような割合 $t$ を計算することで実現しています。この補正処理には前述のルックアップテーブルを使用します。

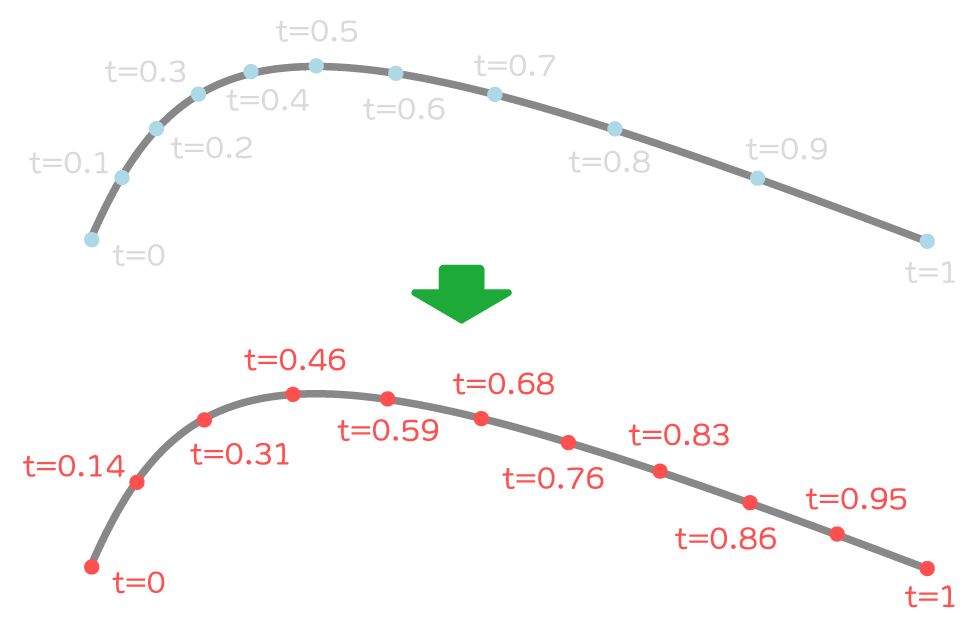
割合を補正した後は、通常通りスプライン曲線における位置などを計算します。

長さに基づいた割合の補正方法

ベジェ曲線上を等速で移動させたい場合、次のような処理で実現できます。

補正処理の流れ

始点からの移動距離を計算する
移動距離とルックアップテーブルより、補正された割合を計算する

スプラインにおける補正処理については後述します。

始点からの移動距離の計算

次式で求められます。

始点からの移動距離を求める式

d = D t

$d$ : 移動距離
$D$ : ベジェ曲線の長さ
$t$ : 割合

補正された割合の取得

移動距離がルックアップテーブル中のどの要素に属するかを調べ、その後、次のような線形補間で近似的な割合を求めます。

割合の補正式

t^{\prime} = t_{i-1} + (t_i - t_{i-1}) \frac{d - d_{i-1}}{d_i - d_{i-1}}

$t^{\prime}$ : 補正された割合
$t_i$ : ルックアップテーブルに属する要素の割合
$t_{i-1}$ : ルックアップテーブルに属する要素の1つ前の割合
$d_i$ : ルックアップテーブルに属する要素の距離
$d_{i-1}$ : ルックアップテーブルに属する要素の1つ前の距離

Splinesパッケージでは、CurveUtility.GetDistanceToInterpolationメソッドより、補正された割合を得ることができます。

public static float GetDistanceToInterpolation<T>(T lut, float distance)
    where T : IReadOnlyList<DistanceToInterpolation>

テンプレート引数Tには、ルックアップテーブルの型を指定します。通常はDistanceToInterpolation型を指定します。

第1引数には、値が格納されたルックアップテーブルを指定します。^[3]

第2引数には、始点からの移動距離を指定します。

戻り値は、補正された割合（範囲0～1）です。

参考：Class CurveUtility | Splines | 1.0.1

サンプルスクリプト

割合の補正前と補正後でベジェ曲線上の位置を取得する比較用スクリプトです。

GetDistanceToInterpolationExample.cs

using UnityEngine;
using UnityEngine.Splines;

public class GetDistanceToInterpolationExample : MonoBehaviour
{
    // 各制御点オブジェクト
    [SerializeField] private Transform _p0Object, _p1Object, _p2Object, _p3Object;

    // 割合
    [SerializeField, Range(0, 1)] private float _t;

    // 補間された位置（割合補正前）
    [SerializeField] private Transform _resultObjectBefore;
    // 補間された位置（割合補正後）
    [SerializeField] private Transform _resultObjectAfter;

    // セグメントの分割数
    [SerializeField] private int _resolution = 30;

    // 各セグメントの点までの長さと割合を格納するルックアップテーブル
    private DistanceToInterpolation[] _lookUpTable;

    private void Awake()
    {
        // ルックアップテーブルを予め作成
        _lookUpTable = new DistanceToInterpolation[_resolution];
    }

    private void Update()
    {
        // 各制御点のワールド座標取得
        var p0 = _p0Object.position;
        var p1 = _p1Object.position;
        var p2 = _p2Object.position;
        var p3 = _p3Object.position;

        // ベジェ曲線定義
        var bezierCurve = new BezierCurve(p0, p1, p2, p3);

        // ルックアップテーブルを取得
        CurveUtility.CalculateCurveLengths(bezierCurve, _lookUpTable);
        
        // ベジェ曲線全体の長さ
        // ルックアップテーブルの末尾要素の距離が長さとなる
        var length = _lookUpTable[^1].Distance;

        // 始点からの移動距離を計算
        var tDistance = length * _t;
        
        // 補正された割合を取得
        var adjustT = CurveUtility.GetDistanceToInterpolation(_lookUpTable, tDistance);

        // 補正前の位置反映
        _resultObjectBefore.position = CurveUtility.EvaluatePosition(
            bezierCurve,
            _t  // 補正前の割合
        );

        // 補正後の位置反映
        _resultObjectAfter.position = CurveUtility.EvaluatePosition(
            bezierCurve,
            adjustT // 補正後の割合
        );
    }
}

上記スクリプトを保存し、適当なゲームオブジェクトにアタッチし、以下のように制御点と結果のオブジェクトを設定すると機能するようになります。

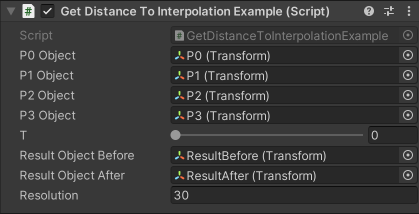
実行結果

以下のように、割合の補正前（黄色キューブ）では速さが変化するのに対し、割合の補正後（赤色キューブ）では速さがほぼ一定になっていることが分かります。

スプライン上の速さを一定にする

ベジェ曲線が繋がったスプライン上の等速移動も、先述のベジェ曲線の等速移動と同様に割合補正を行う流れで実現できます。

補正処理の流れ

始点からの移動距離を計算する
スプライン上のどのベジェ曲線（セグメント）に属するかを移動距離から判定
属するベジェ曲線に対して補正された割合を計算する

補正された割合を求めるAPI

SplineUtility.SplineToCurveTメソッドで求められます。

public static int SplineToCurveT<T>(this T spline, float splineT, out float curveT)
    where T : ISpline

テンプレート引数には、スプラインを管理するクラスの型を指定します。通常はSpline型を指定します。

第1引数には、スプラインのインスタンスを指定します。これは拡張メソッドとして呼び出せます。

第2引数には、補正前の割合を指定します。

第３引数には、補正された比率が結果として格納されます。

戻り値は、どのベジェ曲線に属するかを表すベジェ曲線のインデックスです。

参考：Class SplineUtility | Splines | 1.0.1

このメソッドは、次のようなスプライン上の位置や傾きなどを求めるメソッドで内部的に使用されています。

SplineToCurveTメソッドを使用しているメソッド

SplineUtility.EvaluatePosition
SplineUtility.EvaluateTangent
SplineUtility.EvaluateUpVector
SplineUtility.EvaluateAcceleration
SplineUtility.EvaluateCurvatureCenter

ベジェ曲線の傾き（Tangent）の計算式

ベジェ曲線を割合 $t$ で微分した式になります。

傾きの計算式

\begin{aligned} \bm{v} &= \dfrac{dP}{dt} \\ &= (-3t^2 + 6t - 3) P_0 \\ &\space\space\space\space + (9t^2 - 12t + 3) P_1 \\ &\space\space\space\space + (-9t^2 + 6t) P_2 \\ &\space\space\space\space + 3t^2 P_3 \end{aligned}

上式は、CurveUtility.EvaluateTangentメソッドで内部的に使用されています。

public static float3 EvaluateTangent(BezierCurve curve, float t)

第1引数にベジェ曲線構造体、第2引数に割合を指定します。

戻り値として、傾きのベクトルが返されます。

参考：Class CurveUtility | Splines | 1.0.1

ベジェ曲線の加速度（Acceleration）計算式

傾きの式を更に割合 $t$ で微分した式になります。

加速度の計算式

\begin{aligned} \bm{a} &= \dfrac{d \bm{v}}{dt} \\ &= (- 6t + 6) P_0 \\ &\space\space\space\space + (18t - 12) P_1 \\ &\space\space\space\space + (-18t + 6) P_2 \\ &\space\space\space\space + 6t P_3 \end{aligned}

これは、ベジェ曲線上の位置を割合 $t$ で2階微分することに相当します。

上式は、CurveUtility.EvaluateAccelerationメソッドで内部的に使用されています。

public static float3 EvaluateAcceleration(BezierCurve curve, float t)

形式はCurveUtility.EvaluateTangentメソッドと一緒です。

第1引数にベジェ曲線構造体、第2引数に割合を指定します。

戻り値として、加速度のベクトルが返されます。

参考：Class CurveUtility | Splines | 1.0.1

さいごに

Splinesパッケージのスプライン曲線は、内部的には3次ベジェ曲線の繋がりとして表現されます。

スプライン補間では、速さがほぼ一定になるような補正処理がかけられており、これは近似された曲線の長さに基づいて計算されています。

使用する際の参考にしていただければ幸いです。

【Unity2022】スプラインをスクリプトから扱う方法

Unity公式のビルトインスプラインツール（Splinesパッケージ）で作成したスプラインをスクリプトから読み書きする方法の紹介です。これらの情報は以下公式リファレンスにまとめられています。スプラインとスクリプトを連…

2022年5月17日

【Unity2022】Splinesパッケージの内部計算式

前提条件

ベジェ曲線の補間計算式

補間計算式のヘルパーAPI

サンプルスクリプト

実行結果

ベジェ曲線の長さの計算

近似した長さを求めるヘルパーAPI

サンプルスクリプト

実行結果

距離のルックアップテーブルを取得する

サンプルスクリプト

実行結果

ベジェ曲線上の速さを一定にする

長さに基づいた割合の補正方法

始点からの移動距離の計算

補正された割合の取得

サンプルスクリプト

実行結果

スプライン上の速さを一定にする

補正された割合を求めるAPI

ベジェ曲線の傾き（Tangent）の計算式

ベジェ曲線の加速度（Acceleration）計算式

さいごに

関連記事

参考サイト