次のように紐が交わっているかどうかを知りたいけど、やり方が分からなくって困ってるの…
これは線分同士の交差を判定する数学的問題だわ。
解法が存在するので、今日は線分の交差判定問題について解説していくね！
線分とは
線分とは、2つの点を結ぶ直線のうち、2つの点に挟まれた部分の直線のことです。
両端以降の無限に伸びる部分を含めたものは直線です。
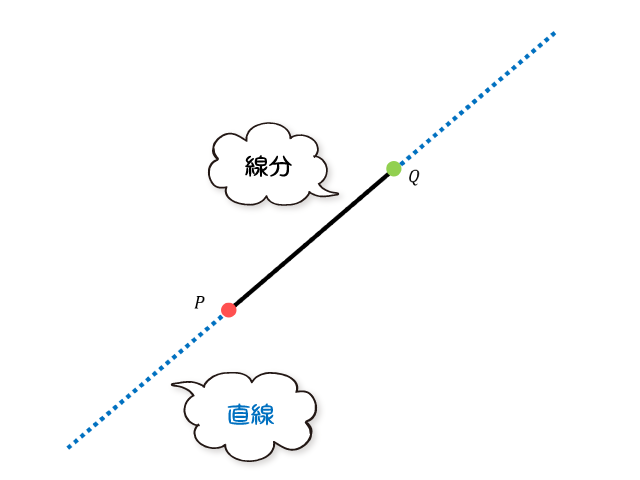
線分は、例えば両端の2点の座標が決まると定まります。
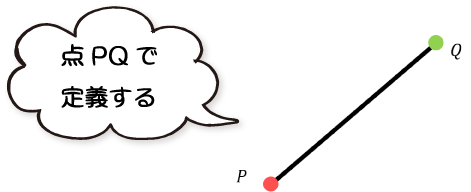
本記事では、両端の2点をP, Qとし、P, Qの座標により定義することにします。
基本的な考え方
線分の交差判定を行うには、判定式を導く必要があります。
本記事では、ベクトル同士の外積を用いて判定式を導く方法をご紹介します。
外積とは
外積は、次式の3次元ベクトル同士の演算で定義されます。
\vec{a} \times\ \vec{b}=(a_yb_z-a_zb_y,a_zb_x-a_xb_z,a_xb_y-a_yb_z)ただし、
\vec{a}=(a_x,a_y,a_z), \vec{b}=(b_x,b_y,b_z)クロス積とも呼ばれ、その演算結果は3次元ベクトルとなります。
2次元ベクトルへの適用
元々、外積は3次元でのみ定義され、2次元ベクトルに対しては定義されません。
2次元ベクトル同士の外積を求めたい場合は、\vec{a}、\vec{b}のz成分を0として外積を適用する方法があります。
このとき、次式のようにa \times\ bのx,y成分は0になります。
\vec{a} \times\ \vec{b}=(0,0,a_xb_y-a_yb_z)ただし、
\vec{a}=(a_x,a_y,0), \vec{b}=(b_x,b_y,0)得られた結果のz成分の符号を見ることで、\vec{a}に対して\vec{b}が左右のどちらに回転しているかを知ることができます。正の場合は反時計回り、負の場合は時計回りに回転していることになります。
外積を使った判定方法
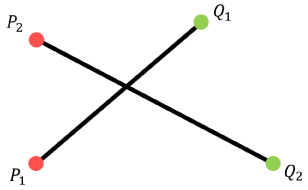
2つの線分をP_1Q_1, P_2Q_2とします。
まず、点P_1からみて、他の点がどのように並んで見えるかをチェックします。
点Q_1がP_2とQ_2の間に見えたら、線分P_1Q_1がもう一方の線分P_2Q_2と交差している可能性が出てきます。
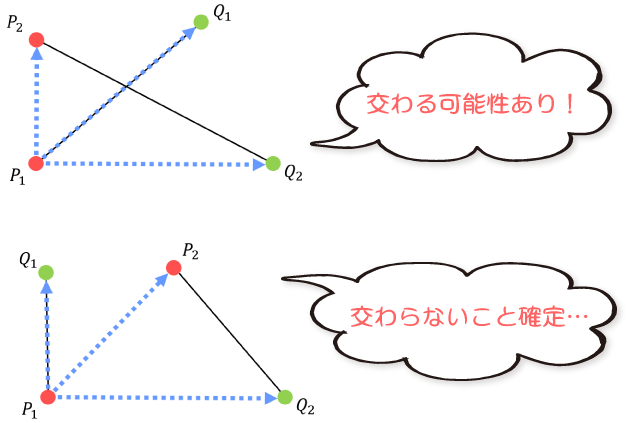
上の条件を満たしたら、同様に点P_2からみて、他の点がどのように並んで見えるかをチェックします。
点Q_2がP_1とQ_1の間に見えたら、線分が交差していることが確定します。
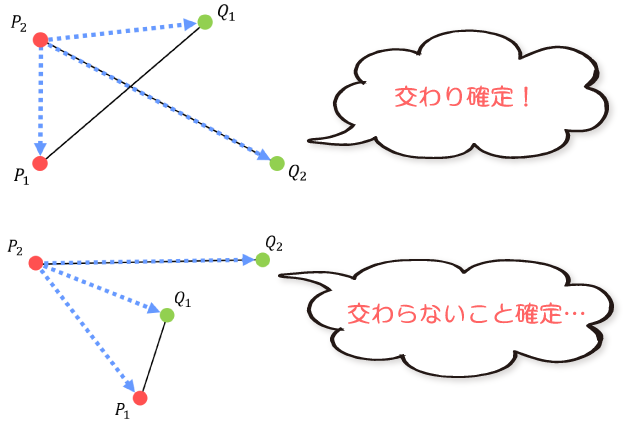
ある点から見た他の点の向き関係は、外積を用いることで確認できます。
判定式は次のようになります。
\vec{P_1Q_1} \times\ \vec{P_1P_2}=(0,0,c_1)\vec{P_1Q_1} \times\ \vec{P_1Q_2}=(0,0,c_2)\vec{P_2Q_2} \times\ \vec{P_2P_1}=(0,0,c_3)\vec{P_2Q_2} \times\ \vec{P_2Q_1}=(0,0,c_4)とすると、線分P_1Q_1, P_2Q_2が交わる条件は、
c_1c_2<0 \land c_3c_4<0
実装例
サンプル
2つの線分の交差判定を行うプログラムの例になります。
Unity用のスクリプトとなります。
#region Logic～#endregionで囲まれた部分が線分の交差判定ロジックになるため、もし利用されたい場合はこの部分から流用してください。
using System;
using UnityEngine;
/// <summary>
/// 線分の交差判定を行うサンプル
/// </summary>
public class LineSegmentChecker : MonoBehaviour
{
// 線分の始点と終点
[Serializable]
private struct Segment
{
public Transform startPoint;
public Transform endPoint;
}
// 線分1
[SerializeField] private Segment _lineSegment1;
// 線分2
[SerializeField] private Segment _lineSegment2;
// 線分1と線分2が交差しているときに表示されるオブジェクト
[SerializeField] private GameObject _crossSign;
// 毎フレーム更新処理
private void Update()
{
// 線分の交差判定
var isCrossing = IsCrossing(
_lineSegment1.startPoint.position, _lineSegment1.endPoint.position,
_lineSegment2.startPoint.position, _lineSegment2.endPoint.position
);
// 交差結果の表示反映
_crossSign.SetActive(isCrossing);
}
#region Logic
// 線分の交差判定
private static bool IsCrossing(Vector2 startPoint1, Vector2 endPoint1, Vector2 startPoint2, Vector2 endPoint2)
{
// ベクトルP1Q1
var vector1 = endPoint1 - startPoint1;
// ベクトルP2Q2
var vector2 = endPoint2 - startPoint2;
//
// 以下条件をすべて満たすときが交差となる
//
// P1Q1 x P1P2 と P1Q1 x P1Q2 が異符号
// かつ
// P2Q2 x P2P1 と P2Q2 x P2Q1 が異符号
//
return Cross(vector1, startPoint2 - startPoint1) * Cross(vector1, endPoint2 - startPoint1) < 0 &&
Cross(vector2, startPoint1 - startPoint2) * Cross(vector2, endPoint1 - startPoint2) < 0;
}
// 2次元ベクトルの外積を返す
private static float Cross(Vector2 vector1, Vector2 vector2)
=> vector1.x * vector2.y - vector1.y * vector2.x;
#endregion
}なお、2次元ベクトルの外積は、結果のz成分のみをfloat型で返すようにしました。
実行結果
さいごに
本記事では、Unityでの実装例をご紹介させていただきましたが、判定ロジック部分はどんなゲームエンジンでもプログラムでも適用できます！
線分交差の判定が出来ればより変化に富んだ衝突判定も実装できるようになることでしょう。
より良いゲーム制作ライフをお過ごしください(^^♪
