【Unity】Time.deltaTimeによる移動の原理

こじゃらこじゃら

どうして移動にTime.deltaTimeを使う必要があるの？

本当にフレームレートに依存しない移動になるかも詳しく知りたいの。

このはこのは

原理について順を追って解説していくね。フレームレートによる動きの違いも見ていくわ。

Unityで登場するTime.deltaTimeは、前フレームからの経過時間[s]を表すプロパティです。

この経過時間を用いた移動処理を実装することで、結果としてフレームレート（1秒間に描画される回数）による動きの差異をある程度なくすことが可能です。

// 移動速度[m/s]
Vector3 velocity;

・・・（中略）・・・

private void Update()
{
    // 移動
    transform.position += velocity * Time.deltaTime;
}

ただし、厳密に差異がなくなる訳ではなく、計算誤差の蓄積による差異が生じます。

フレームレート違いによる誤差蓄積の例

この誤差を許容するか否かは、状況によって変わってくるでしょう。例えば、フィールドを動くキャラクターなどは誤差は気になりませんが、レール上を動くギミックなどは位置ずれが目立ってしまうかもしれません。

このように、ある値に時間（デルタタイム）を掛けた値を、位置に対して加算していくような実装は、「速度」と「時間」という物理量に基づいた移動処理を実装していることに等しいです。

本記事では、Time.deltaTimeプロパティを用いて移動処理が実現できる理由について解説していきます。また、フレームレートが変化した際の挙動の違いと計算誤差による差異の蓄積についても検証していきます。

動作環境
  • Unity 2022.2.16f1

スポンサーリンク

目次 非表示

前提条件

本記事では、時間・時刻を[s]（秒）、距離を[m]（メートル）、速さ・速度を[m/s]（メートル毎秒）として単位を扱う事とします。

Unityの位置の単位はUnity unitとされており、デフォルトではメートルとして扱われます。 [1]

本記事で扱う位置や距離の単位は、このデフォルト単位であるメートルとします。

また、本記事はtransform.positionの更新による移動を対象とするため、Rigidbodyによる移動は取り扱いません。

Time.deltaTimeの基本仕様

前回フレームから現在フレームまでの時間[s]を返すプロパティです。

処理落ちなどでフレームレートが低下すると、このTime.deltaTimeプロパティの値も大きくなります。

ただし、Time.maximumDeltaTime以上にならないように制限が設けられています。

これによって、極端な処理落ちでキャラクターがワープしてしまうような現象を防ぐことが可能です。

また、Time.timeScaleの値によって時間の進行速度が変わり、Time.deltaTimeの値は元の経過時間にTime.timeScaleを掛けた結果となります。 [2]

速度と時間に基づいた移動量の計算

デルタタイムによる移動処理は、移動量を求める計算に基づくものです。

移動量の計算式は、速度と時間と距離の関係から導くことができます。

速さから移動距離を求める

速さとは、単位時間あたりにどれくらいの距離を移動するかを表す物理量です。1[s]間に移動する距離[m]が速さ[m/s]となります。

速さを一定とすると、移動距離[m]は速さ[m/s]に経過時間[s]を掛けることで計算できます。

移動距離を求める式
\Delta x = s \Delta t

ただし、

\Delta x : 移動距離[s]、s : 速さ[m/s]、\Delta t : 経過時間[t]

例えば、3つのオブジェクトで速さがそれぞれ1[m/s]、2[m/s]、3[m/s]の時、以下のように時間あたりの移動距離も比例して増えます。

フレームレートが30FPSの場合はデルタタイムが\dfrac{1}{30} \approx 0.033[s]、60FPSの場合はデルタタイムが\dfrac{1}{60} \approx 0.016[s]という風にフレームレートに反比例して小さくなっていきます。

このように、フレームレートに応じて経過時間（デルタタイム）が変化するため、結果としてフレームレートに依存しない挙動が実現できます。

速度から移動量を求める

速度とは、速さ（大きさ）と向きを持った物理量です。Unityで実際に扱うのはこちらになるでしょう。

プログラム中ではfloat型（1次元）、Vector2型（2次元）、Vector3型（3次元）などの値として扱うことになります。 [3]

どの向きにどれくらいの距離を移動したかを表す移動量[m]は、速度[m/s]と経過時間[s]を用いて次式のように計算できます。

移動量の計算式
\Delta P = \vec{v} \Delta t

ただし、

\Delta P : 移動量[m]、\vec{v} : 速度[m/s]、\Delta t : 経過時間[m]

ここでも速度は一定で変わらないものとします。

速度が異なると、移動距離や向きもまちまちです。

現在位置の計算

前述の移動量は、ある時間においてどの向きにどの距離だけ移動したかを表す物理量[m]です。

現在位置を求めるためには、初期位置を定める必要があります。初期位置をP_0とすると、\Delta t[s]後の位置Pは次式のように計算できます。

位置の計算式
P = P_0 + \vec{v} \Delta t

Time.deltaTimeを用いた移動処理の実装

ここまでの流れを踏まえ、実装方法の解説に入ります。

前述の速度と時間に基づく移動は、Updateイベントなどで現在位置の計算処理を繰り返し行うことで実現できます。

このとき、数式の各パラメータは、次のようにコード中の変数やプロパティに対応します。

数式パラメータとコードとの対応関係

P_0 : 変更する前（前回フレーム）のtransform.positionプロパティ。

\vec{v} : 移動速度を格納する変数。例えばVector3型の変数などが該当。

\Delta t : Time.deltaTimeプロパティ。

P : 上記の計算結果。最終的にtransform.positionプロパティに代入される。

初期位置P_0は前回フレームの位置とみなすことが出来ます。

実際のコードに落とし込むと次のようになります。

// 現在位置[m] = 前回位置[m] + 速度[m/s] * 時間[s]
transform.position = transform.position + _velocity * Time.deltaTime;
// より簡潔な書き方
transform.position += _velocity * Time.deltaTime;

サンプルスクリプト

以下、自身のオブジェクトを指定した速度で移動させ続ける例です。

VelocityMovement.cs
using UnityEngine;

public class VelocityMovement : MonoBehaviour
{
    // 移動速度[m/s]
    [SerializeField] private Vector3 _velocity;

    private void Update()
    {
        // 前フレーム位置と速度と経過時間から、現在位置を計算する
        transform.position += _velocity * Time.deltaTime;
    }
}

上記をVelocityMovement.csという名前でUnityプロジェクトに保存し、移動対象のオブジェクトにアタッチし、インスペクタより移動速度を設定すると機能するようになります。

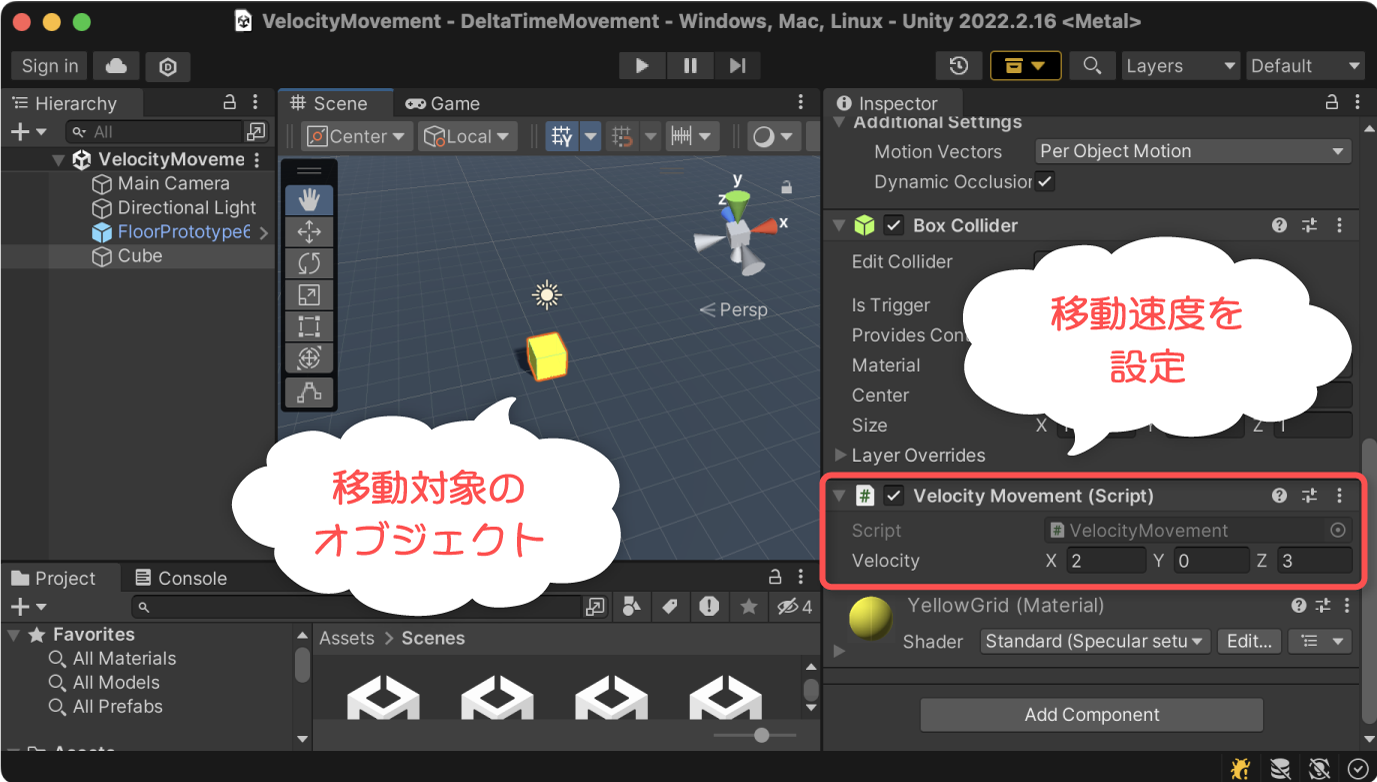
実行結果

指定した移動速度で移動するようになりました。

例えば、フレームレートを2FPS（0.5秒おき更新）に変更しても、見かけ上の移動速度は一致しています。

フレームレートの違いによる計算誤差

ここまでフレームレートが変わっても見た目上動きが変わらないことが確認できました。

しかしながら、厳密に一致するとは限りません。

例えば、プレイヤーを操作する場合、フレームレートが異なると以下のように位置ずれが蓄積していきます。

このようになってしまう理由は、フレーム間の移動は等速直線運動として近似していること、そもそも足し合わせる移動量が異なっていることなどが挙げられます。

そのため、等速直線運動するオブジェクト同士でフレームレートを変えてみると、ほぼ位置ずれが起きないことが確認できます。

ただし、それでも僅かながら誤差は蓄積していきます。理由は、浮動小数点の加算演算を行う際に丸め誤差が発生するためです。

誤差の蓄積を防ぐ方法

前述のような誤差の蓄積を防ぐ手段はいくつかありますが、代表的なのはフレーム毎の加算処理を無くし、計算式によって時間から一意に値を求めることでしょう。

等速直線運動の場合

例えば、等速直線運動（等速度運動）の場合は次のように位置を求めることが出来ます。

等速直線運動の位置計算式
P = P_0 + \vec{v} t

ただし、

P : 位置[m]、P_0 : 初期位置[m]、\vec{v} : 速度[m/s]、t : 移動開始からの時間[s]

コードに落とし込むと次のようになります。

UniformLinearMotion.cs
using UnityEngine;

public class UniformLinearMotion : MonoBehaviour
{
    // 移動速度[m/s]
    // ※ただし、この速度は常に一定であるという前提
    [SerializeField] private Vector3 _constantVelocity;

    // 初期位置[m]
    private Vector3 _startPosition;

    // 時刻[s]
    private float _time;

    private void Start()
    {
        // 初期位置を記録しておく
        _startPosition = transform.position;
    }

    private void Update()
    {
        // 時刻更新
        _time += Time.deltaTime;

        // 現在位置を計算して反映する
        transform.position = _startPosition + _constantVelocity * _time;
    }
}

以下部分で現在フレームの位置を開始位置に基づいて計算しているため、誤差が蓄積しません。

// 現在位置を計算して反映する
transform.position = _startPosition + _constantVelocity * _time;

等加速度運動の場合

等加速度運動とは、常に一定の加速度がかかる運動のことを指します。

加速度（ベクトル）を\vec{a}とすると、\Delta t経過したときの速度変化量\Delta \vec{v}は次式のように計算されます。

速度の変化量を求める式
\Delta \vec{v} = \vec{a} \Delta t

これは、単位時間当たりの速度の変化量である加速度[m/s^2]が発生するためです。

現在速度\vec{v}は、初速度\vec{v_0}を用いて次式で計算できます。

速度を求める式
\vec{v} = \vec{v_0} + \vec{a} \Delta t

等加速度運動による移動処理をコードに落とし込むと次のようになります。

// 加速度[m/s^2]
Vector3 acceleration;
// 現在速度[m/s]
Vector3 velocity;

・・・（中略）・・・

private void Update()
{
    // 加速度から速度を求める
    velocity += acceleration * Time.deltaTime;

    // 速度から位置を求める
    transform.position += velocity * Time.deltaTime;
}

このような計算処理は、次式に変換することで誤差の蓄積を無くせます。

等加速度運動の位置計算式
P = P_0 + \vec{v_0} t + \frac{1}{2} \vec{a} t^2

実際のコードは以下のようになります。

MotionOfUniformAcceleration.cs
using UnityEngine;

public class MotionOfUniformAcceleration : MonoBehaviour
{
    // 加速度[m/s^2]
    // ※ただし、この加速度は常に一定であるという前提
    [SerializeField] private Vector3 _constantAcceleration;

    // 初速度[m/s]
    [SerializeField] private Vector3 _initialVelocity;

    // 初期位置[m]
    private Vector3 _startPosition;

    // 時刻[s]
    private float _time;

    private void Start()
    {
        // 初期位置を記録しておく
        _startPosition = transform.position;
    }

    private void Update()
    {
        // 時刻更新
        _time += Time.deltaTime;

        // 現在位置を計算して反映する
        transform.position =
            _startPosition +
            _initialVelocity * _time +
            0.5f * _constantAcceleration * _time * _time;
    }
}

ただし、開始位置を基準として動かすため融通が利かないという制約もあります。

メモ

UnityのアニメーションやTween系アセット、Splinesパッケージなどで実装される移動処理も基本的に計算式から一意に位置を求めます。

そのため、時間経過に伴う誤差の蓄積を防ぐことが可能です。

積分との関係

等速直線運動や等加速度運動などで、誤差の蓄積を防ぐための計算式が出てきましたが、これは速度や加速度を時間積分して求められる式です。

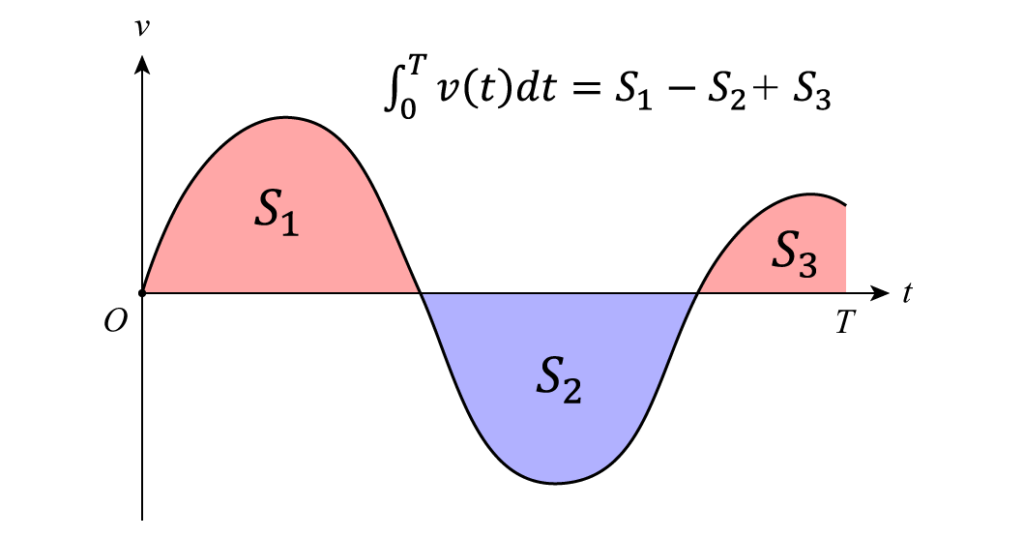
デルタタイムによってフレーム毎の位置を求める計算は、次のように横軸を時間、縦軸を速度としたグラフの面積（ただし負の部分は減算する）を求めることに等しいです。

v-tグラフと位置の計算

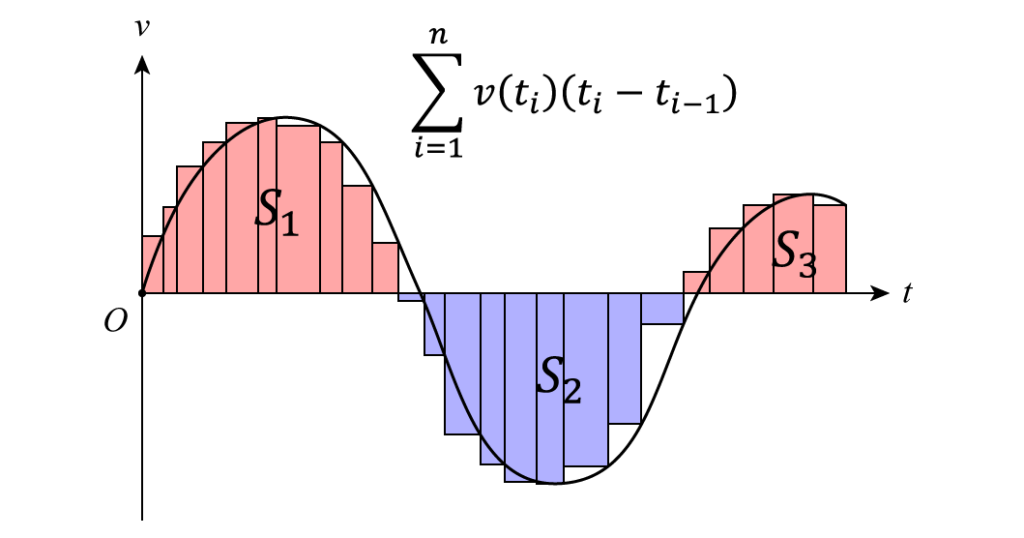
プログラム上では、各矩形の横幅が各フレームにおけるTime.deltaTimeに相当します。 [4]

このデルタタイムの幅を0に限りなく近づけた極限値が定積分です。

速度と定積分

等速直線運動の位置計算式の導出

n次関数を積分すると次式のようになります。

n次関数の積分公式
\displaystyle \int x^ndx = \frac{1}{n+1} x^{n+1} + C

ただし、

Cは積分定数、n \ne -1

等速直線運動は、積分により次式のように位置の計算式を導き出せます。

\begin{aligned}
P(t) &= \displaystyle \int \vec{v}dt \\
&= \vec{v} t + C
\end{aligned}

ここで、初期位置P(0) = P_0とすると、

P(0) = P_0  = C

したがって、

P(t) = P_0 + \vec{v} t

等加速度運動の位置計算式の導出

速度\vec{v}(t)は、加速度\vec{a}を時間積分した結果となります。

\begin{aligned}
\vec{v}(t) &= \displaystyle \int \vec{a}dt \\
&= \vec{a} t + C
\end{aligned}

ここで、\vec{v}(0) = \vec{v_0}とすると、

\vec{v}(t) = \vec{v_0} + \vec{a} t

位置は更に速度を時間積分して求めます。

\begin{aligned}
P(t) &= \displaystyle \int \vec{v}dt \\
&= \displaystyle \int (\vec{v_0} + \vec{a} t)dt \\
&=  \vec{v_0}t + \frac{1}{2} \vec{a}t^2 + C
\end{aligned}

ここで、初期位置P(0) = P_0とすると、

P(t) = P_0 + \vec{v_0}t + \frac{1}{2} \vec{a}t^2

検証用スクリプト

以下、積分で求めた計算式とデルタタイムを足し合わせることによる結果の比較用スクリプトです。

CompareExample.cs
using UnityEngine;

public class CompareExample : MonoBehaviour
{
    [Header("等速直線運動のパラメータ")]

    // 移動速度[m/s]
    [SerializeField]
    private Vector3 _velocity;

    // 初期位置[m]
    [SerializeField] private Vector3 _startPosition;

    [Header("加速度運動のパラメータ")]
    // 加速度[m/s^2]
    [SerializeField]
    private Vector3 _acceleration;

    // 初速度[m/s]
    [SerializeField] private Vector3 _initialVelocity;

    [Header("表示用オブジェクト")]

    // 等速直線運動
    [SerializeField]
    private Transform _linerMotionObject;

    // 等速直線運動（積分による計算）
    [SerializeField] private Transform _linerMotionObjectIntegral;

    // 加速度運動
    [SerializeField] private Transform _accelerationMotionObject;

    // 加速度運動（積分による計算）
    [SerializeField] private Transform _accelerationMotionObjectIntegral;

    private float _time;
    private Vector3 _currentVelocity;

    private void Start()
    {
        _currentVelocity = _initialVelocity;
    }

    // 各オブジェクトのローカル位置を更新する
    private void Update()
    {
        // 現在時刻計算
        _time += Time.deltaTime;

        // 等速直線運動
        _linerMotionObject.localPosition = _startPosition + _velocity * _time;

        // 等速直線運動（積分による計算）
        _linerMotionObjectIntegral.localPosition = _startPosition + _velocity * _time;

        // 加速度運動
        _currentVelocity += _acceleration * Time.deltaTime;
        _accelerationMotionObject.localPosition += _currentVelocity * Time.deltaTime;

        // 加速度運動（積分による計算）
        _accelerationMotionObjectIntegral.localPosition =
            _startPosition +
            _initialVelocity * _time +
            0.5f * _acceleration * _time * _time;
    }
}

上記をCompareExample.csという名前でUnityプロジェクトに保存し、適当なゲームオブジェクトにアタッチし、インスペクタよりパラメータと表示用オブジェクトを設定すると機能します。

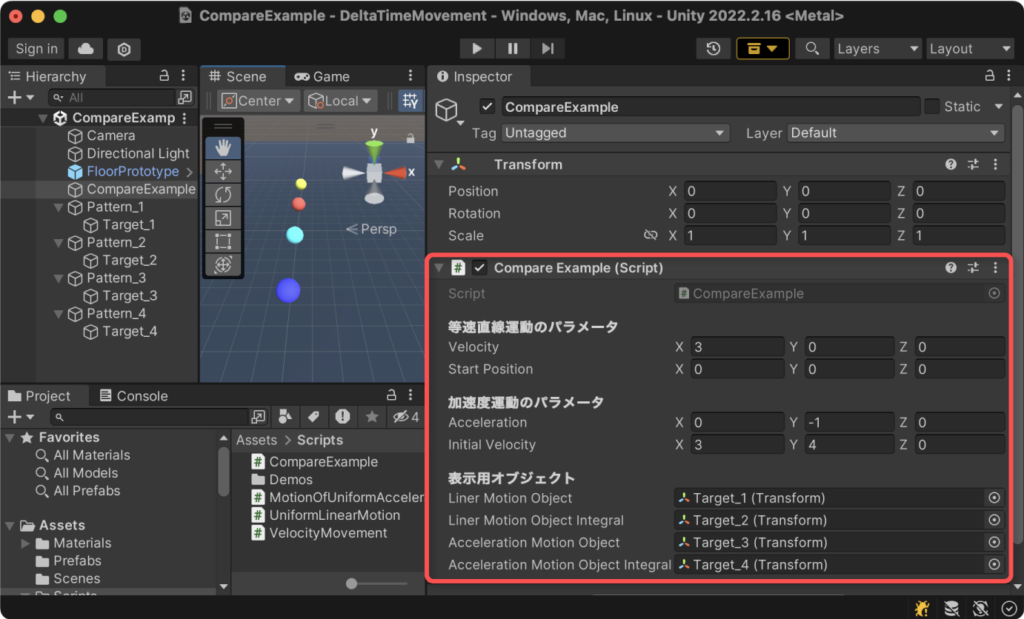
実行結果

等速直線運動するオブジェクト同士、等加速度運動するオブジェクト同士で動きが一致していることが確認できました。

さいごに

Time.deltaTimeを用いた移動処理は、指定した速度でオブジェクトを移動する処理を実装しています。

このような時間と速度に基づいて毎フレームの位置を計算する手法は、Unity以外の場面でも普遍的に活用できるテクニックです。

ただし、時間経過により計算誤差が蓄積していくことを理解しておくとより安全でしょう。

関連記事

参考サイト

スポンサーリンク

前の記事

【Unity】Actionの指定を便利にするInputActi…

次の記事

【Unity】Cinemachineカメラをスプラインに沿って…